# [LCP 46. 志愿者调配](https://leetcode.cn/problems/05ZEDJ) ## 题目描述 <!-- 这里写题目描述 --> 「力扣挑战赛」有 `n` 个比赛场馆(场馆编号从 `0` 开始),场馆之间的通道分布情况记录于二维数组 `edges` 中,`edges[i]= [x, y]` 表示第 `i` 条通道连接场馆 `x` 和场馆 `y`(即两个场馆相邻)。初始每个场馆中都有一定人数的志愿者(不同场馆人数可能不同),后续 `m` 天每天均会根据赛事热度进行志愿者人数调配。调配方案分为如下三种: 1. 将编号为 `idx` 的场馆内的志愿者人数减半; 2. 将编号为 `idx` 的场馆相邻的场馆的志愿者人数都加上编号为 `idx` 的场馆的志愿者人数; 3. 将编号为 `idx` 的场馆相邻的场馆的志愿者人数都减去编号为 `idx` 的场馆的志愿者人数。 所有的调配信息记录于数组 `plans` 中,`plans[i] = [num,idx]` 表示第 `i` 天对编号 `idx` 的场馆执行了第 `num` 种调配方案。 在比赛结束后对调配方案进行复盘时,不慎将第 `0` 个场馆的**最终**志愿者人数丢失,只保留了**初始**所有场馆的志愿者总人数 `totalNum` ,以及记录了第 `1 ~ n-1` 个场馆的**最终**志愿者人数的一维数组 `finalCnt`。请你根据现有的信息求出初始每个场馆的志愿者人数,并按场馆编号顺序返回志愿者人数列表。 **注意:** - 测试数据保证当某场馆进行第一种调配时,该场馆的志愿者人数一定为偶数; - 测试数据保证当某场馆进行第三种调配时,该场馆的相邻场馆志愿者人数不为负数; - 测试数据保证比赛开始时每个场馆的志愿者人数都不超过 `10^9`; - 测试数据保证给定的场馆间的道路分布情况中不会出现自环、重边的情况。 **示例 1:** >  > 输入: > `finalCnt = [1,16], totalNum = 21, edges = [[0,1],[1,2]], plans = [[2,1],[1,0],[3,0]]` > > 输出:`[5,7,9]` > > 解释: > 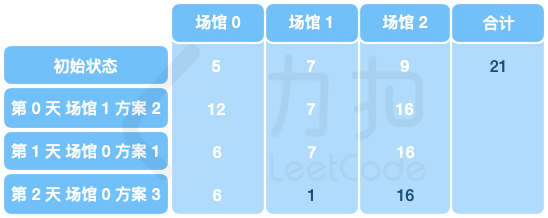 **示例 2 :** > 输入: > `finalCnt = [4,13,4,3,8], totalNum = 54, edges = [[0,3],[1,3],[4,3],[2,3],[2,5]], plans = [[1,1],[3,3],[2,5],[1,0]]` > > 输出:`[10,16,9,4,7,8]` **提示:** - `2 <= n <= 5*10^4` - `1 <= edges.length <= min((n * (n - 1)) / 2, 5*10^4)` - `0 <= edges[i][0], edges[i][1] < n` - `1 <= plans.length <= 10` - `1 <= plans[i][0] <=3` - `0 <= plans[i][1] < n` - `finalCnt.length = n-1` - `0 <= finalCnt[i] < 10^9` - `0 <= totalNum < 5*10^13` ## 解法 <!-- 这里可写通用的实现逻辑 --> <!-- tabs:start --> ### **Python3** <!-- 这里可写当前语言的特殊实现逻辑 --> ```python ``` ### **Java** <!-- 这里可写当前语言的特殊实现逻辑 --> ```java ``` ### **...** ``` ``` <!-- tabs:end -->