You are given a 0-indexed m x n integer matrix grid and an integer k. You are currently at position (0, 0) and you want to reach position (m - 1, n - 1) moving only down or right.
Return the number of paths where the sum of the elements on the path is divisible by k. Since the answer may be very large, return it modulo 109 + 7.
Example 1:
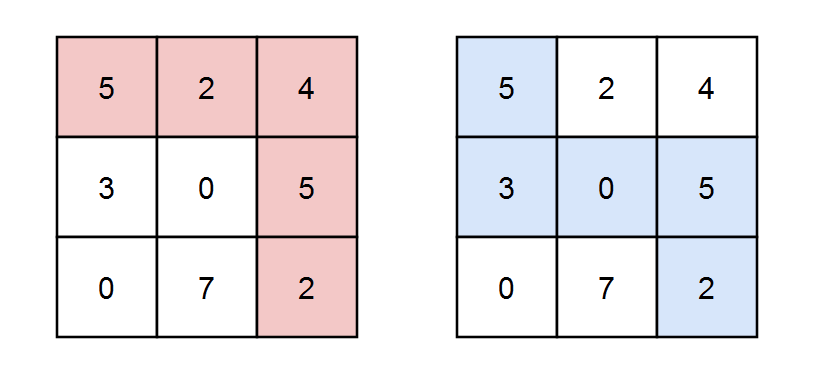
Input: grid = [[5,2,4],[3,0,5],[0,7,2]], k = 3 Output: 2 Explanation: There are two paths where the sum of the elements on the path is divisible by k. The first path highlighted in red has a sum of 5 + 2 + 4 + 5 + 2 = 18 which is divisible by 3. The second path highlighted in blue has a sum of 5 + 3 + 0 + 5 + 2 = 15 which is divisible by 3.
Example 2:
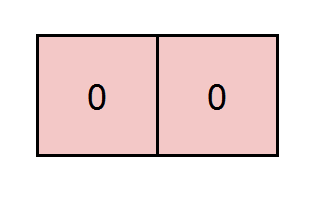
Input: grid = [[0,0]], k = 5 Output: 1 Explanation: The path highlighted in red has a sum of 0 + 0 = 0 which is divisible by 5.
Example 3:
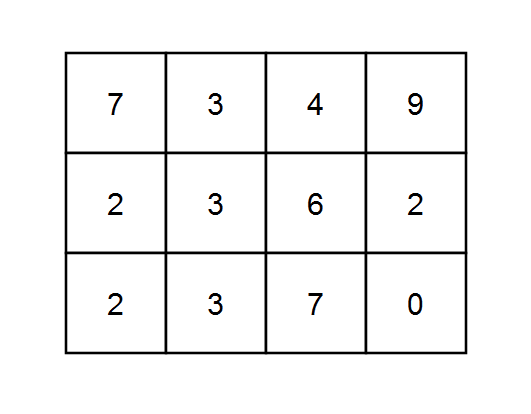
Input: grid = [[7,3,4,9],[2,3,6,2],[2,3,7,0]], k = 1 Output: 10 Explanation: Every integer is divisible by 1 so the sum of the elements on every possible path is divisible by k.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 5 * 1041 <= m * n <= 5 * 1040 <= grid[i][j] <= 1001 <= k <= 50
class Solution:
def numberOfPaths(self, grid: List[List[int]], k: int) -> int:
@cache
def dfs(i, j, s):
if i < 0 or i >= m or j < 0 or j >= n:
return 0
s = (s + grid[i][j]) % k
if i == m - 1 and j == n - 1:
return int(s == 0)
ans = dfs(i + 1, j, s) + dfs(i, j + 1, s)
return ans % mod
m, n = len(grid), len(grid[0])
mod = 10**9 + 7
ans = dfs(0, 0, 0)
dfs.cache_clear()
return ansclass Solution:
def numberOfPaths(self, grid: List[List[int]], k: int) -> int:
m, n = len(grid), len(grid[0])
dp = [[[0] * k for _ in range(n)] for _ in range(m)]
dp[0][0][grid[0][0] % k] = 1
mod = 10**9 + 7
for i in range(m):
for j in range(n):
for s in range(k):
t = ((s - grid[i][j] % k) + k) % k
if i:
dp[i][j][s] += dp[i - 1][j][t]
if j:
dp[i][j][s] += dp[i][j - 1][t]
dp[i][j][s] %= mod
return dp[-1][-1][0]class Solution {
private int m;
private int n;
private int k;
private static final int MOD = (int) 1e9 + 7;
private int[][] grid;
private int[][][] f;
public int numberOfPaths(int[][] grid, int k) {
this.grid = grid;
this.k = k;
m = grid.length;
n = grid[0].length;
f = new int[m][n][k];
for (var a : f) {
for (var b : a) {
Arrays.fill(b, -1);
}
}
return dfs(0, 0, 0);
}
private int dfs(int i, int j, int s) {
if (i < 0 || i >= m || j < 0 || j >= n) {
return 0;
}
s = (s + grid[i][j]) % k;
if (f[i][j][s] != -1) {
return f[i][j][s];
}
if (i == m - 1 && j == n - 1) {
return s == 0 ? 1 : 0;
}
int ans = dfs(i + 1, j, s) + dfs(i, j + 1, s);
ans %= MOD;
f[i][j][s] = ans;
return ans;
}
}class Solution {
private static final int MOD = (int) 1e9 + 7;
public int numberOfPaths(int[][] grid, int k) {
int m = grid.length, n = grid[0].length;
int[][][] dp = new int[m][n][k];
dp[0][0][grid[0][0] % k] = 1;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
for (int s = 0; s < k; ++s) {
int t = ((s - grid[i][j] % k) + k) % k;
if (i > 0) {
dp[i][j][s] += dp[i - 1][j][t];
}
if (j > 0) {
dp[i][j][s] += dp[i][j - 1][t];
}
dp[i][j][s] %= MOD;
}
}
}
return dp[m - 1][n - 1][0];
}
}class Solution {
public:
int numberOfPaths(vector<vector<int>>& grid, int k) {
int m = grid.size(), n = grid[0].size();
int mod = 1e9 + 7;
vector<vector<vector<int>>> f(m, vector<vector<int>>(n, vector<int>(k, -1)));
function<int(int, int, int)> dfs;
dfs = [&](int i, int j, int s) {
if (i < 0 || i >= m || j < 0 || j >= n) return 0;
s = (s + grid[i][j]) % k;
if (i == m - 1 && j == n - 1) return s == 0 ? 1 : 0;
if (f[i][j][s] != -1) return f[i][j][s];
int ans = dfs(i + 1, j, s) + dfs(i, j + 1, s);
ans %= mod;
f[i][j][s] = ans;
return ans;
};
return dfs(0, 0, 0);
}
};class Solution {
public:
const int mod = 1e9 + 7;
int numberOfPaths(vector<vector<int>>& grid, int k) {
int m = grid.size(), n = grid[0].size();
vector<vector<vector<int>>> dp(m, vector<vector<int>>(n, vector<int>(k)));
dp[0][0][grid[0][0] % k] = 1;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
for (int s = 0; s < k; ++s) {
int t = ((s - grid[i][j] % k) + k) % k;
if (i) dp[i][j][s] += dp[i - 1][j][t];
if (j) dp[i][j][s] += dp[i][j - 1][t];
dp[i][j][s] %= mod;
}
}
}
return dp[m - 1][n - 1][0];
}
};func numberOfPaths(grid [][]int, k int) int {
m, n := len(grid), len(grid[0])
var mod int = 1e9 + 7
f := make([][][]int, m)
for i := range f {
f[i] = make([][]int, n)
for j := range f[i] {
f[i][j] = make([]int, k)
for x := 0; x < k; x++ {
f[i][j][x] = -1
}
}
}
var dfs func(i, j, s int) int
dfs = func(i, j, s int) int {
if i < 0 || i >= m || j < 0 || j >= n {
return 0
}
s = (s + grid[i][j]) % k
if i == m-1 && j == n-1 {
if s == 0 {
return 1
}
return 0
}
if f[i][j][s] != -1 {
return f[i][j][s]
}
ans := dfs(i+1, j, s) + dfs(i, j+1, s)
ans %= mod
f[i][j][s] = ans
return ans
}
return dfs(0, 0, 0)
}func numberOfPaths(grid [][]int, k int) int {
m, n := len(grid), len(grid[0])
var mod int = 1e9 + 7
dp := make([][][]int, m)
for i := range dp {
dp[i] = make([][]int, n)
for j := range dp[i] {
dp[i][j] = make([]int, k)
}
}
dp[0][0][grid[0][0]%k] = 1
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
for s := 0; s < k; s++ {
t := ((s - grid[i][j]%k) + k) % k
if i > 0 {
dp[i][j][s] += dp[i-1][j][t]
}
if j > 0 {
dp[i][j][s] += dp[i][j-1][t]
}
dp[i][j][s] %= mod
}
}
}
return dp[m-1][n-1][0]
}function numberOfPaths(grid: number[][], k: number): number {
const MOD = 10 ** 9 + 7;
const m = grid.length,
n = grid[0].length;
let ans = Array.from({ length: m + 1 }, () =>
Array.from({ length: n + 1 }, () => new Array(k).fill(0)),
);
ans[0][1][0] = 1;
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
for (let v = 0; v < k; v++) {
let key = (grid[i][j] + v) % k;
ans[i + 1][j + 1][key] =
(ans[i][j + 1][v] +
ans[i + 1][j][v] +
ans[i + 1][j + 1][key]) %
MOD;
}
}
}
return ans[m][n][0];
}