Skip to content

Latest commit

 

History

History
310 lines (175 loc) · 11.9 KB

数据结构.md

File metadata and controls

310 lines (175 loc) · 11.9 KB

数据结构

常见的数据结构:

  • 数组(Array)
  • 栈(Stack)
  • 队列(Queue)
  • 链表(LinkedList)
  • 树(Tree)
  • 哈希表(Hash)
  • 堆(Heap)
  • 图(Graph)

数组(Array)

数组是一种大小固定的数据结构，对线性表的所有操作都可以通过数组来实现。数组是在内存中开辟一段连续的空间，并在此空间存放元素。就像是一排出租屋，有100个房间，从001到100每个房间都有固定编号，通过编号就可以快速找到租房子的人。虽然数组一旦创建之后，它的大小就无法改变了，但是当数组不能再存储线性表中的新元素时，我们可以创建一个新的大的数组来替换当前数组。这样就可以使用数组实现动态的数据结构。

int[] arr = new int[10];

数组是最常用的数据结构了。这里就不说了。

优点:

  • 可以通过下标来访问或者修改元素，比较高效

缺点:

  • 增删慢，插入和删除的花费开销比较大，比如当在第一个位置前插入一个元素，那么首先要把所有的元素往后移动一个位置
  • 大小固定，只能存储单一元素，

栈(Stack)

The Stack class represents a last-in-first-out (LIFO) stack of objects. It extends class Vector with five operations that allow a vector to be treated as a stack. The usual push and pop operations are provided, as well as a method to peek at the top item on the stack, a method to test for whether the stack is empty, and a method to search the stack for an item and discover how far it is from the top. When a stack is first created, it contains no items.

栈是限制插入和删除只能在一个位置上进行的表，该位置是表的末端，叫作栈顶，数据称为压栈，移除数据称为弹栈(就像子弹弹夹装弹和取弹一样)。 对栈的基本操作有push(进栈)和pop(出栈)，前者相当于插入，后者相当于删除最后一个元素。栈有时又叫作LIFO(Last In First Out)表， 即后进先出。简单暴力的理解就是吃进去吐出来

优点:

  • 提供了先进后出的存取方式

缺点:

  • 存取其他项很慢

队列(Queue)

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端(front)进行删除操作，而在表的后端(rear)进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。先进先出，简单暴力的理解就是吃进去拉出来

优点:

  • 提供了先进先出的存取方式

缺点:

  • 存取其他项很慢

链表(LinkedList)

链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。 链表由一系列结点（链表中每一个元素称为结点）组成，结点可以在运行时动态生成。 每个结点包括两个部分：一个是存储数据元素的数据域，另一个是存储下一个结点地址的指针域。 相比于线性表顺序结构，链表比较方便插入和删除操作。

用一组地址任意的存储单元存放线性表中的数据元素。以元素(数据元素的映象)+指针(指示后继元素存储位置) = 结点。 以“结点的序列”表示线性表,称作线性链表（单链表）。单链表是一种顺序存取的结构，为找第i个数据元素，必须先找到第i-1个数据元素。

链表的结点结构:

         ┌──┬──┐──┐
         │data│next│
         └──┴──┘──┘

data域:存放结点值的数据域 　　 next域:存放结点的直接后继的地址（位置）的指针域（链域）。

注意:

  • 链表通过每个结点的链域将线性表的n个结点按其逻辑顺序链接在一起的。 　　
  • 每个结点只有一个链域的链表称为单链表(Single Linked List)

所谓的链表就好像火车车厢一样，从火车头开始，每一节车厢之后都连着后一节车厢。

优点:

  • 和数组相比，链表的优势在于长度不受限制，也不需要连续的内存空间。
  • 在进行插入和删除操作时，不需要移动数据项，故尽管某些操作的时间复杂度与数组想同，实际效率上还是比数组要高很多,所以插入快，删除快

缺点:

  • 劣势在于随机访问，无法像数组那样直接通过下标找到特定的数据项
  • 查找慢
  • 相对数组只存储元素，链表的元素还要存储其他元素地址，内存开销相对增大

树(Tree)

树是由n（n>=1）个有限节点组成一个具有层次关系的集合。
它具有以下特点:每个节点有零个或多个子节点；没有父节点的节点称为根节点；每一个非根节点有且只有一个父节点；除了根节点外，每个子节点可以分为多个不相交的子树。

二叉树

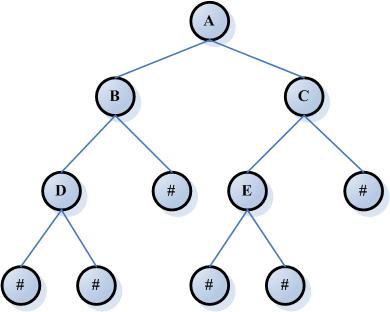
二叉树(binary tree)是一棵树，每一个节点都不能有多于两个的子节点。
通常子树被称作“左子树”和“右子树”。二叉树常被用于实现二叉查找树和二叉堆。

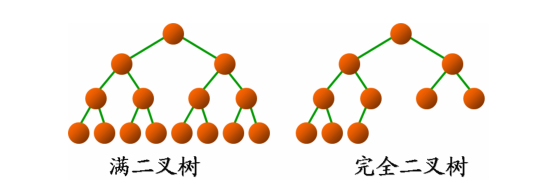
image

满二叉树和完全二叉树

满二叉树:除最后一层无任何子节点外，每一层上的所有结点都有两个子结点。也可以这样理解，除叶子结点外的所有结点均有两个子结点。节点数达到最大值，所有叶子结点必须在同一层上。

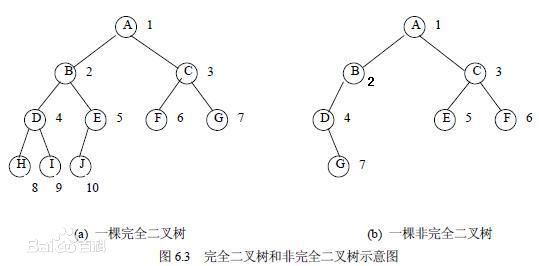
完全二叉树:若设二叉树的深度为h，除第h层外，其它各层(1～(h-1))层的结点数都达到最大个数，第h层所有的结点都连续集中在最左边，这就是完全二叉树。

image

完全二叉树是效率很高的数据结构，堆是一种完全二叉树或者近似完全二叉树，所以效率极高，像十分常用的排序算法、Dijkstra算法、Prim算法等都要用堆才能优化，二叉排序树的效率也要借助平衡性来提高，而平衡性基于完全二叉树。

image

我们知道一颗基本的二叉排序树他们都需要满足一个基本性质：即树中的任何节点的值大于它的左子节点，且小于它的右子节点。

按照这个基本性质使得树的检索效率大大提高。我们知道在生成二叉排序树的过程是非常容易失衡的，最坏的情况就是一边倒（只有右/左子树），这样势必会导致二叉树的检索效率大大降低(O(n))，所以为了维持二叉排序树的平衡，大牛们提出了各种平衡二叉树的实现算法，在平衡二叉搜索树中，其高度一般都良好地维持在O(log2n)，大大降低了操作的时间复杂度。如：AVL，SBT，伸展树，TREAP ，红黑树等等。

平衡二叉树

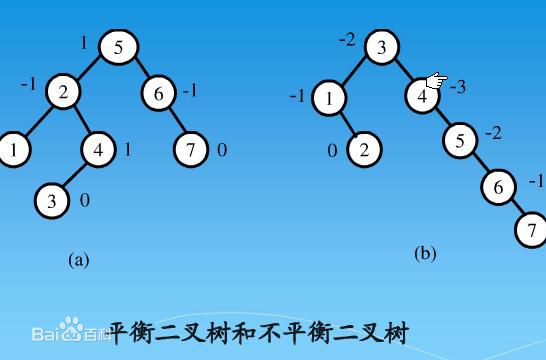
平衡二叉树必须具备如下特性：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。也就是说该二叉树的任何一个子节点，其左右子树的高度都相近。下面给出平衡二叉树的示意图：

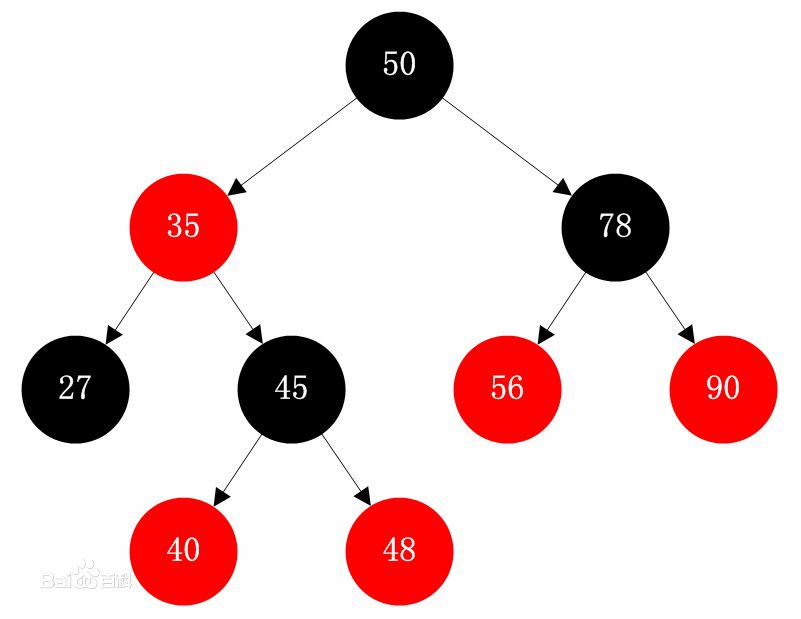
image

红黑树

红黑树顾名思义就是结点是红色或者是黑色的平衡二叉树，它通过颜色的约束来维持着二叉树的平衡。红黑树是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。它是在1972年由Rudolf Bayer发明的，他称之为"对称二叉B树"，它现代的名字是在Leo J. Guibas和Robert Sedgewick于1978年写的一篇论文中获得的。它是复杂的，但它的操作有着良好的最坏情况运行时间，并且在实践中是高效的: 它可以在O(log n)时间内做查找，插入和删除，这里的n是树中元素的数目。

对于一棵有效的红黑树而言我们必须增加如下规则，这也是红黑树最重要的5点规则:

  • 每个结点都只能是红色或者黑色中的一种。
  • 根结点是黑色的。
  • 每个叶结点（NIL节点，空节点）是黑色的。
  • 如果一个结点是红的，则它两个子节点都是黑的。也就是说在一条路径上不能出现相邻的两个红色结点。
  • 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结

这些约束强制了红黑树的关键性质: 从根到叶子最长的可能路径不多于最短的可能路径的两倍长。结果是这棵树大致上是平衡的。

image

黑红树节点的java表示结构:

private static final boolean RED = true;
private static final boolean BLACK = false;
private Node root;//二叉查找树的根节点

//结点数据结构
private class Node{
    private Key key;//键
    private Value value;//值
    private Node left, right;//指向子树的链接:左子树和右子树.
    private int N;//以该节点为根的子树中的结点总数
    boolean color;//由其父结点指向它的链接的颜色也就是结点颜色.

    public Node(Key key, Value value, int N, boolean color) {
        this.key = key;
        this.value = value;
        this.N = N;
        this.color = color;
    }
}

/**
 * 获取整个二叉查找树的大小
 * @return
 */
public int size(){
    return size(root);
}
/**
 * 获取某一个结点为根结点的二叉查找树的大小
 * @param x
 * @return
 */
private int size(Node x){
    if(x == null){
        return 0;
    } else {
        return x.N;
    }
}
private boolean isRed(Node x){
    if(x == null){
        return false;
    }
    return x.color == RED;
}

哈希表(Hash)

哈希表就是一种以 键-值(key-indexed)存储数据的结构，我们只要输入待查找的值即key，即可查找到其对应的值。

优点:

  • 如果关键字已知则存取极快
  • 插入、查找、删除的时间级为O(1)
  • 数据项占哈希表长的一半，或者三分之二时，哈希表的性能最好。

缺点:

  • 删除慢，如果不知道关键字存取慢，对存储空间使用不充分
  • 基于数组，数组创建后难于扩展，某些哈希表被基本填满时性能下降的非常严重；
  • 没有一种简单的方法可以以任何一种顺序（如从小到大）遍历整个数据项；

堆(Heap)

这里所说的堆是数据结构中的堆，而不是内存模型中的堆。堆通常是一个可以被看做一棵树，它满足下列性质:

  • 堆中任意节点的值总是不大于(不小于)其子节点的值；
  • 堆是完全二叉树
  • 常常用数组实现

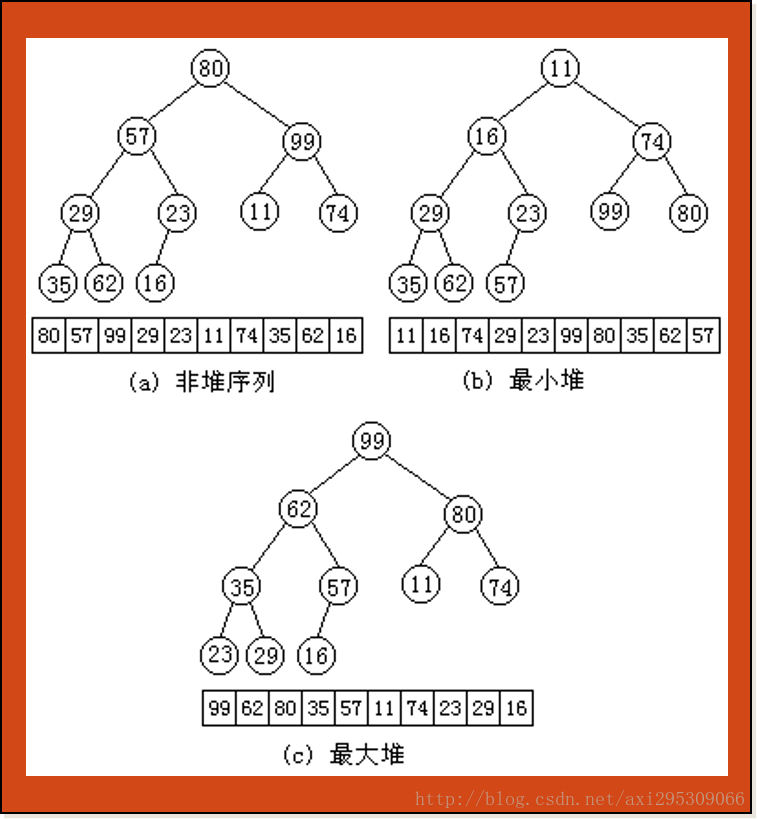
image

二叉堆是完全二元树或者是近似完全二元树，它分为两种：最大堆和最小堆。 最大堆：父结点的键值总是大于或等于任何一个子节点的键值；最小堆：父结点的键值总是小于或等于任何一个子节点的键值。

优点:

  • 插入、删除快，对最大数据项存取快

缺点:

  • 对其他数据项存取慢

图(Graph)

图是一种较线性表和树更为复杂的数据结构，在线性表中，数据元素之间仅有线性关系，在树形结构中，数据元素之间有着明显的层次关系，而在图形结构中，节点之间的关系可以是任意的，图中任意两个数据元素之间都可能相关。图的应用相当广泛，特别是近年来的迅速发展，已经渗入到诸如语言学、逻辑学、物理、化学、电讯工程、计算机科学以及数学的其他分支中。

优点:

  • 对现实世界建模

缺点:

  • 有些算法慢且复杂