一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
给定一个 m x n 的整数数组 grid。一个机器人初始位于 左上角（即 grid[0][0]）。机器人尝试移动到 右下角（即 grid[m - 1][n - 1]）。机器人每次只能向下或者向右移动一步。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。
+网格中的障碍物和空位置分别用 1 和 0 来表示。机器人的移动路径中不能包含 任何 有障碍物的方格。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？
+返回机器人能够到达右下角的不同路径数量。
-网格中的障碍物和空位置分别用 1 和 0 来表示。
测试用例保证答案小于等于 2 * 109。
diff --git a/solution/0100-0199/0191.Number of 1 Bits/README.md b/solution/0100-0199/0191.Number of 1 Bits/README.md index 646ac1b15b9a9..c8981ee6b9a56 100644 --- a/solution/0100-0199/0191.Number of 1 Bits/README.md +++ b/solution/0100-0199/0191.Number of 1 Bits/README.md @@ -42,7 +42,7 @@ tags:
输入：n = 2147483645 输出：30 -解释：输入的二进制串 11111111111111111111111111111101 中，共有 30 个设置位。+解释：输入的二进制串 1111111111111111111111111111101 中，共有 30 个设置位。
diff --git a/solution/0300-0399/0314.Binary Tree Vertical Order Traversal/README_EN.md b/solution/0300-0399/0314.Binary Tree Vertical Order Traversal/README_EN.md index 2d9746559e7df..6ca291e4cedbc 100644 --- a/solution/0300-0399/0314.Binary Tree Vertical Order Traversal/README_EN.md +++ b/solution/0300-0399/0314.Binary Tree Vertical Order Traversal/README_EN.md @@ -27,24 +27,24 @@ tags:
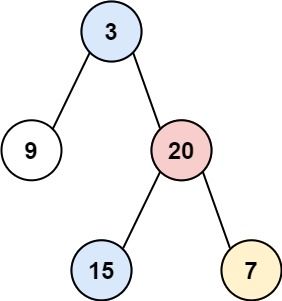
Example 1:
-
+
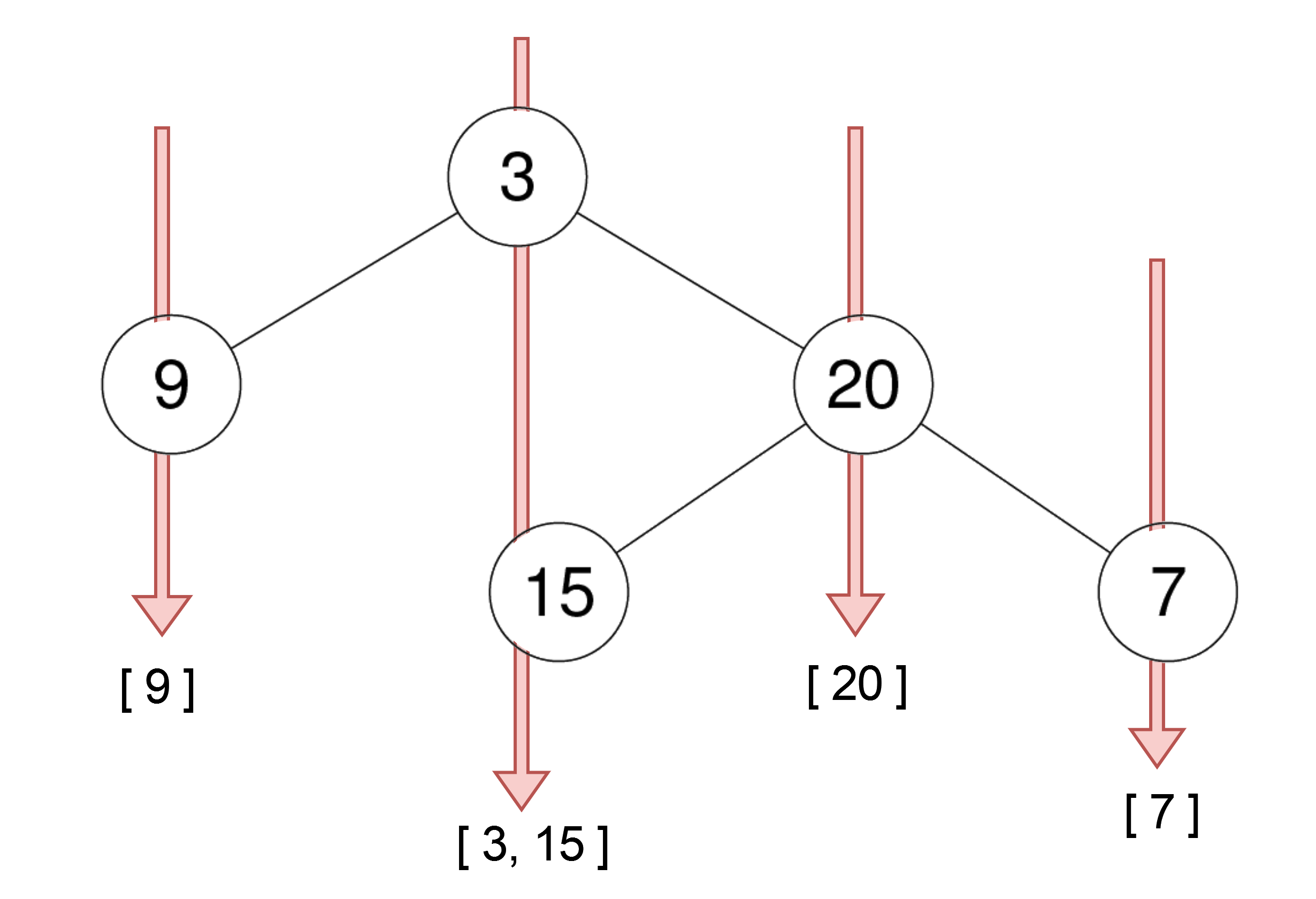
Input: root = [3,9,20,null,null,15,7] Output: [[9],[3,15],[20],[7]]
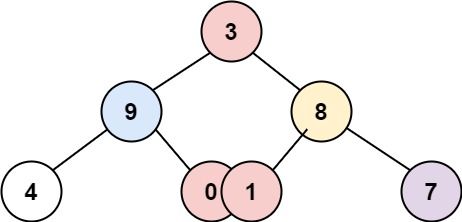
Example 2:
-
+
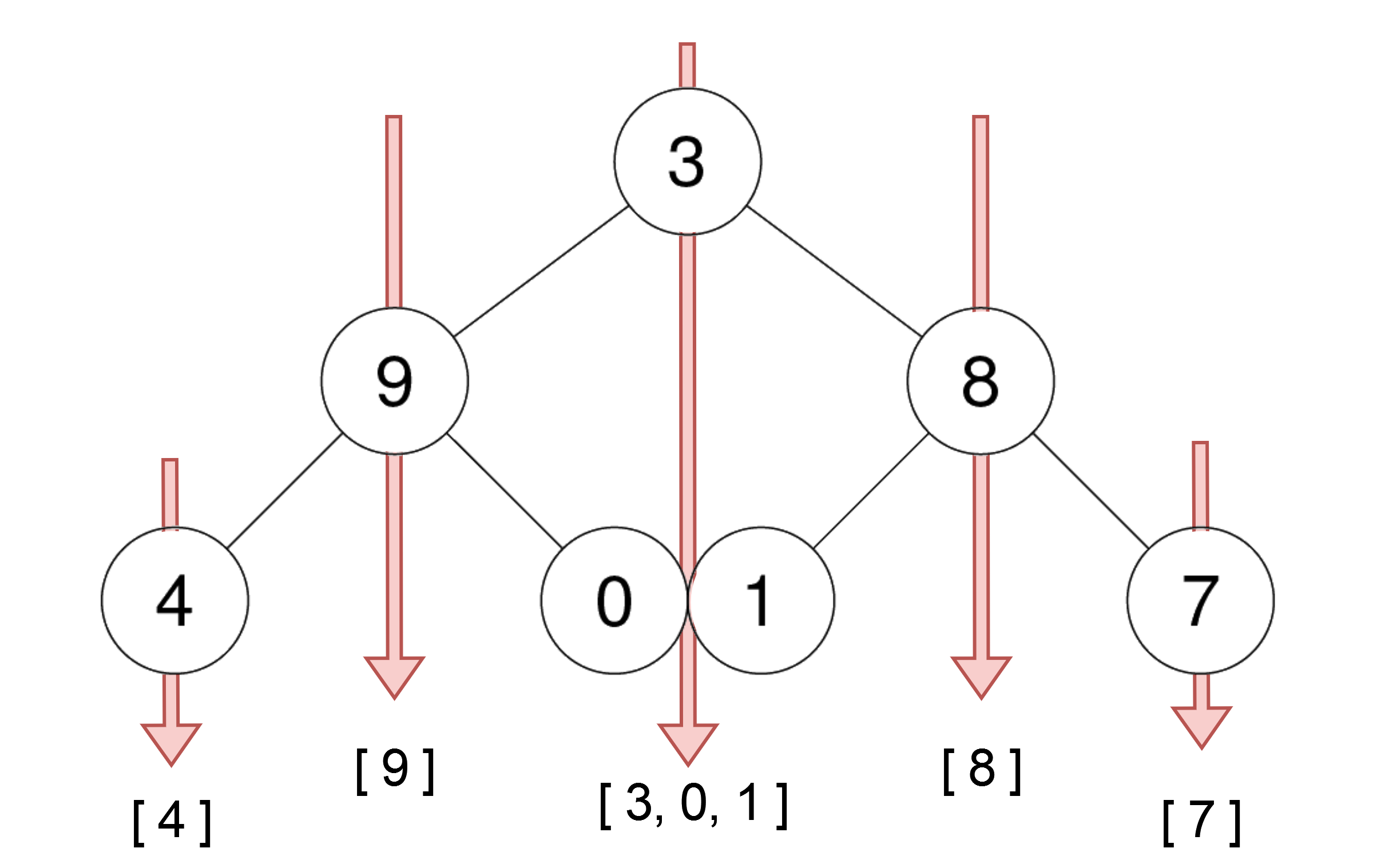
Input: root = [3,9,8,4,0,1,7] Output: [[4],[9],[3,0,1],[8],[7]]
Example 3:
-
+
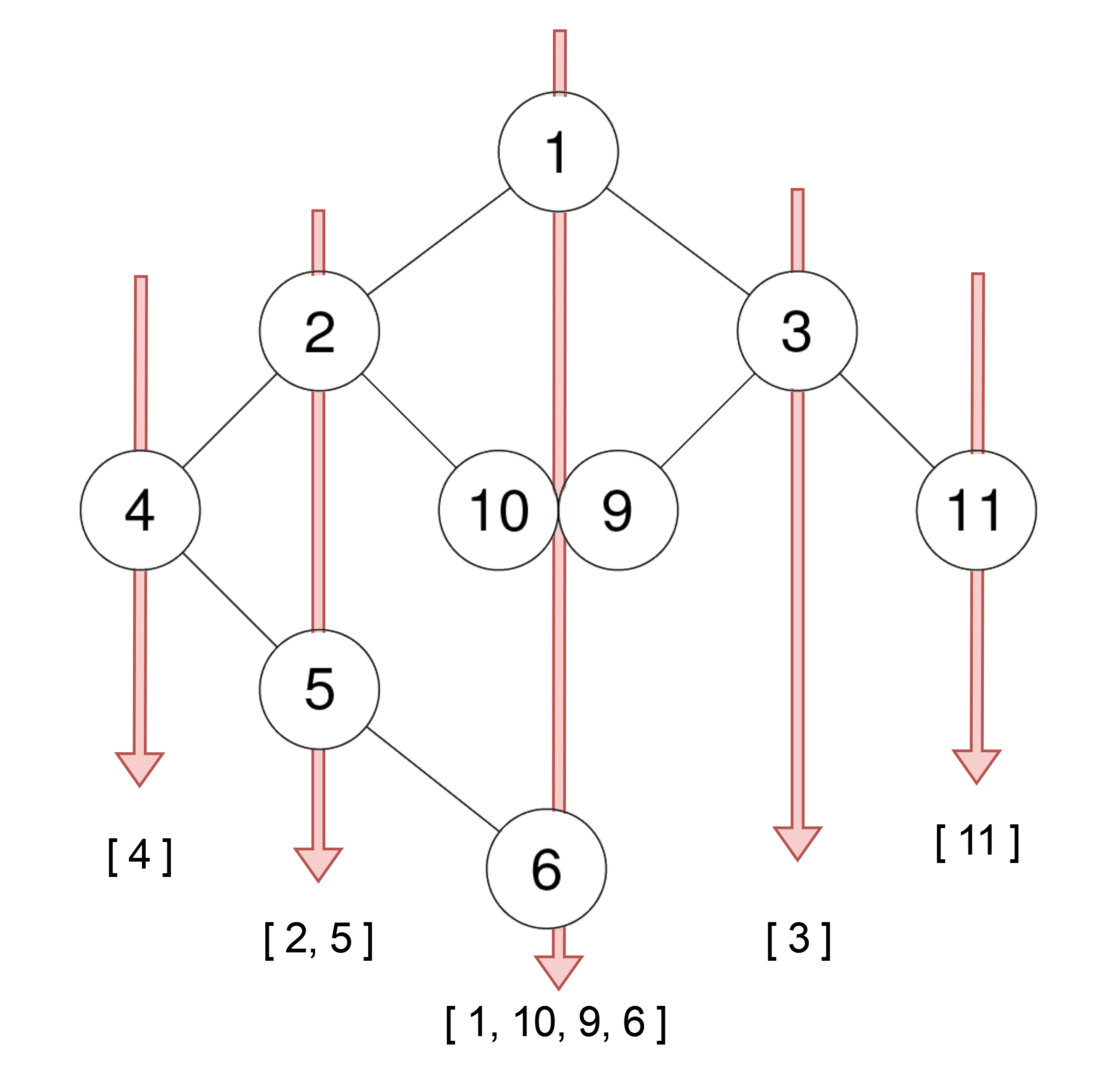
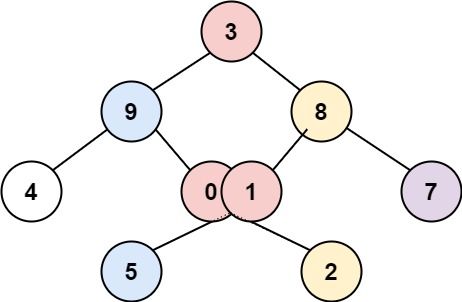
-Input: root = [3,9,8,4,0,1,7,null,null,null,2,5] -Output: [[4],[9,5],[3,0,1],[8,2],[7]] +Input: root = [1,2,3,4,10,9,11,null,5,null,null,null,null,null,null,null,6] +Output: [[4],[2,5],[1,10,9,6],[3],[11]]
diff --git a/solution/0300-0399/0314.Binary Tree Vertical Order Traversal/images/image1.png b/solution/0300-0399/0314.Binary Tree Vertical Order Traversal/images/image1.png new file mode 100644 index 0000000000000..46e4f25ba56b2 Binary files /dev/null and b/solution/0300-0399/0314.Binary Tree Vertical Order Traversal/images/image1.png differ diff --git a/solution/0300-0399/0314.Binary Tree Vertical Order Traversal/images/image2.png b/solution/0300-0399/0314.Binary Tree Vertical Order Traversal/images/image2.png new file mode 100644 index 0000000000000..4eb9ab14b9c60 Binary files /dev/null and b/solution/0300-0399/0314.Binary Tree Vertical Order Traversal/images/image2.png differ diff --git a/solution/0300-0399/0314.Binary Tree Vertical Order Traversal/images/image3.png b/solution/0300-0399/0314.Binary Tree Vertical Order Traversal/images/image3.png new file mode 100644 index 0000000000000..93d9124fb4d40 Binary files /dev/null and b/solution/0300-0399/0314.Binary Tree Vertical Order Traversal/images/image3.png differ diff --git a/solution/0400-0499/0428.Serialize and Deserialize N-ary Tree/README.md b/solution/0400-0499/0428.Serialize and Deserialize N-ary Tree/README.md index c2f6edf1659a8..8470025cbdde7 100644 --- a/solution/0400-0499/0428.Serialize and Deserialize N-ary Tree/README.md +++ b/solution/0400-0499/0428.Serialize and Deserialize N-ary Tree/README.md @@ -27,7 +27,7 @@ tags:
-
@@ -35,7 +35,7 @@ tags:
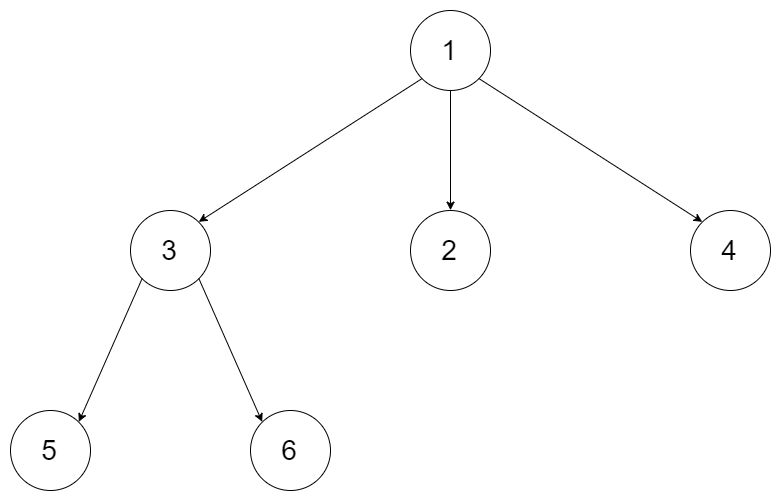
或者，您可以遵循 LeetCode 的层序遍历序列化格式，其中每组孩子节点由空值分隔。
-
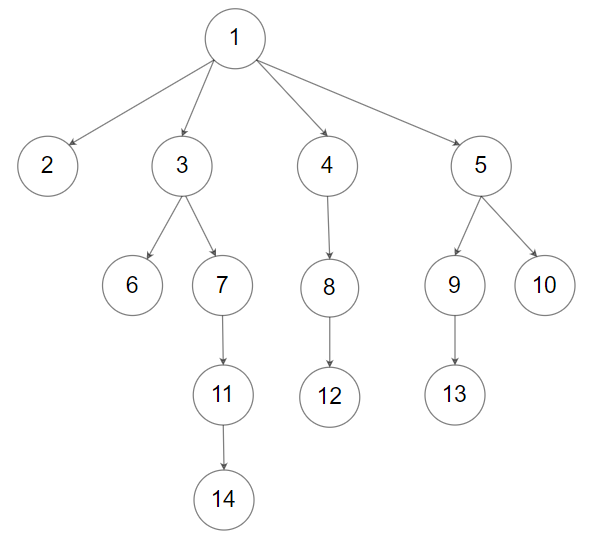
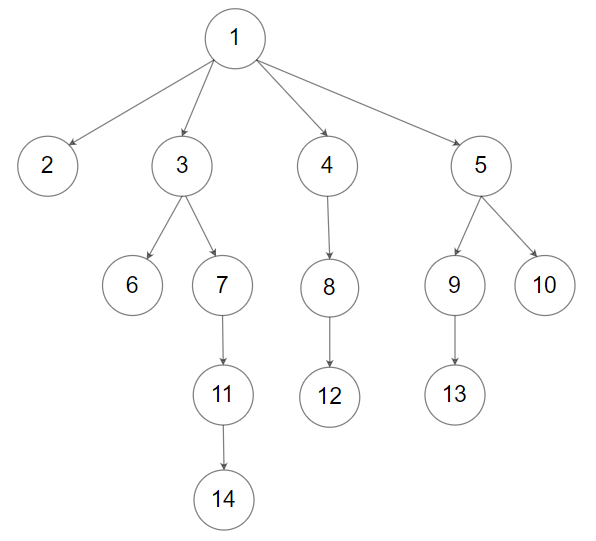
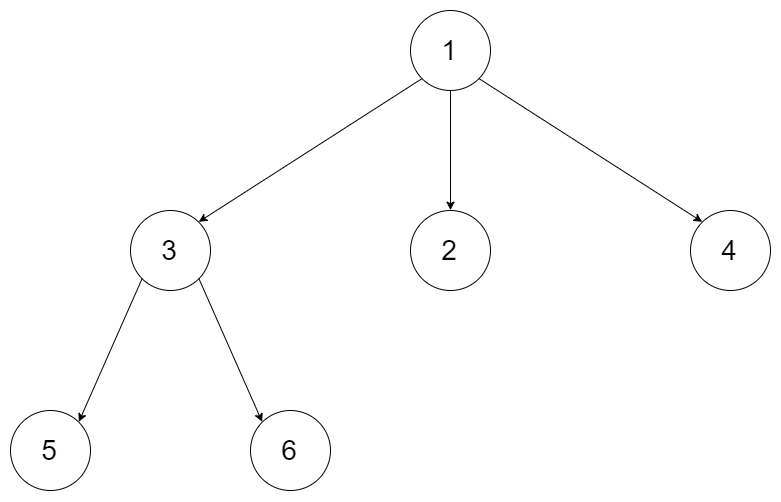
例如，上面的树可以序列化为 [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
emails[i] 都包含有且仅有一个 '@' 字符'+' 字符作为开头".com" 后缀结尾。".com" 后缀前至少包含一个字符'+' character.".com" suffix.".com" suffix.各查询结果的评分与其位置之间比率的平均值。
-将劣质查询百分比 poor_query_percentage 为：
将劣质查询百分比 poor_query_percentage 定义为：
评分小于 3 的查询结果占全部查询结果的百分比。
diff --git a/solution/1500-1599/1560.Most Visited Sector in a Circular Track/README.md b/solution/1500-1599/1560.Most Visited Sector in a Circular Track/README.md index f99453ef12efd..ddf06acb0535c 100644 --- a/solution/1500-1599/1560.Most Visited Sector in a Circular Track/README.md +++ b/solution/1500-1599/1560.Most Visited Sector in a Circular Track/README.md @@ -69,6 +69,14 @@ tags: ### 方法一：考虑开始、结束的位置关系 +由于每个阶段的结束位置是下一个阶段的开始位置，并且每个阶段都是逆时针方向的，所以我们可以根据开始和结束的位置关系来确定每个扇区的经过次数。 + +如果 $\textit{rounds}[0] \leq \textit{rounds}[m]$，那么从 $\textit{rounds}[0]$ 开始，到 $\textit{rounds}[m]$ 结束的所有扇区经过的次数是最多的，我们可以直接返回这个区间内的所有扇区。 + +否则，从 $1$ 开始，到 $\textit{rounds}[m]$ 结束的所有扇区和从 $\textit{rounds}[0]$ 开始，到 $n$ 结束的所有扇区的并集是经过次数最多的，我们可以返回这两个区间的并集。 + +时间复杂度 $O(n)$，其中 $n$ 是扇区的个数。忽略答案数组的空间消耗，空间复杂度 $O(1)$。 + #### Python3 @@ -114,10 +122,16 @@ public: int m = rounds.size() - 1; vectorans; if (rounds[0] <= rounds[m]) { - for (int i = rounds[0]; i <= rounds[m]; ++i) ans.push_back(i); + for (int i = rounds[0]; i <= rounds[m]; ++i) { + ans.push_back(i); + } } else { - for (int i = 1; i <= rounds[m]; ++i) ans.push_back(i); - for (int i = rounds[0]; i <= n; ++i) ans.push_back(i); + for (int i = 1; i <= rounds[m]; ++i) { + ans.push_back(i); + } + for (int i = rounds[0]; i <= n; ++i) { + ans.push_back(i); + } } return ans; } @@ -146,6 +160,28 @@ func mostVisited(n int, rounds []int) []int { } ``` +#### TypeScript + +```ts +function mostVisited(n: number, rounds: number[]): number[] { + const ans: number[] = []; + const m = rounds.length - 1; + if (rounds[0] <= rounds[m]) { + for (let i = rounds[0]; i <= rounds[m]; ++i) { + ans.push(i); + } + } else { + for (let i = 1; i <= rounds[m]; ++i) { + ans.push(i); + } + for (let i = rounds[0]; i <= n; ++i) { + ans.push(i); + } + } + return ans; +} +``` + diff --git a/solution/1500-1599/1560.Most Visited Sector in a Circular Track/README_EN.md b/solution/1500-1599/1560.Most Visited Sector in a Circular Track/README_EN.md index 0e1ba33cf82ad..daf6bce342e90 100644 --- a/solution/1500-1599/1560.Most Visited Sector in a Circular Track/README_EN.md +++ b/solution/1500-1599/1560.Most Visited Sector in a Circular Track/README_EN.md @@ -66,7 +66,15 @@ We can see that both sectors 1 and 2 are visited twice and they are the most vis -### Solution 1 +### Solution 1: Considering the Relationship Between Start and End Positions + +Since the end position of each stage is the start position of the next stage, and each stage is in a counterclockwise direction, we can determine the number of times each sector is passed based on the relationship between the start and end positions. + +If $\textit{rounds}[0] \leq \textit{rounds}[m]$, then the sectors from $\textit{rounds}[0]$ to $\textit{rounds}[m]$ are passed the most times, and we can directly return all sectors within this interval. + +Otherwise, the sectors from $1$ to $\textit{rounds}[m]$ and the sectors from $\textit{rounds}[0]$ to $n$ form the union of the most passed sectors, and we can return the union of these two intervals. + +The time complexity is $O(n)$, where $n$ is the number of sectors. Ignoring the space consumption of the answer array, the space complexity is $O(1)$. @@ -113,10 +121,16 @@ public: int m = rounds.size() - 1; vector ans; if (rounds[0] <= rounds[m]) { - for (int i = rounds[0]; i <= rounds[m]; ++i) ans.push_back(i); + for (int i = rounds[0]; i <= rounds[m]; ++i) { + ans.push_back(i); + } } else { - for (int i = 1; i <= rounds[m]; ++i) ans.push_back(i); - for (int i = rounds[0]; i <= n; ++i) ans.push_back(i); + for (int i = 1; i <= rounds[m]; ++i) { + ans.push_back(i); + } + for (int i = rounds[0]; i <= n; ++i) { + ans.push_back(i); + } } return ans; } @@ -145,6 +159,28 @@ func mostVisited(n int, rounds []int) []int { } ``` +#### TypeScript + +```ts +function mostVisited(n: number, rounds: number[]): number[] { + const ans: number[] = []; + const m = rounds.length - 1; + if (rounds[0] <= rounds[m]) { + for (let i = rounds[0]; i <= rounds[m]; ++i) { + ans.push(i); + } + } else { + for (let i = 1; i <= rounds[m]; ++i) { + ans.push(i); + } + for (let i = rounds[0]; i <= n; ++i) { + ans.push(i); + } + } + return ans; +} +``` + diff --git a/solution/1500-1599/1560.Most Visited Sector in a Circular Track/Solution.cpp b/solution/1500-1599/1560.Most Visited Sector in a Circular Track/Solution.cpp index 32cea27587cd8..2d1219a0eebaa 100644 --- a/solution/1500-1599/1560.Most Visited Sector in a Circular Track/Solution.cpp +++ b/solution/1500-1599/1560.Most Visited Sector in a Circular Track/Solution.cpp @@ -4,11 +4,17 @@ class Solution { int m = rounds.size() - 1; vector ans; if (rounds[0] <= rounds[m]) { - for (int i = rounds[0]; i <= rounds[m]; ++i) ans.push_back(i); + for (int i = rounds[0]; i <= rounds[m]; ++i) { + ans.push_back(i); + } } else { - for (int i = 1; i <= rounds[m]; ++i) ans.push_back(i); - for (int i = rounds[0]; i <= n; ++i) ans.push_back(i); + for (int i = 1; i <= rounds[m]; ++i) { + ans.push_back(i); + } + for (int i = rounds[0]; i <= n; ++i) { + ans.push_back(i); + } } return ans; } -}; \ No newline at end of file +}; diff --git a/solution/1500-1599/1560.Most Visited Sector in a Circular Track/Solution.ts b/solution/1500-1599/1560.Most Visited Sector in a Circular Track/Solution.ts new file mode 100644 index 0000000000000..4aef02a74ae68 --- /dev/null +++ b/solution/1500-1599/1560.Most Visited Sector in a Circular Track/Solution.ts @@ -0,0 +1,17 @@ +function mostVisited(n: number, rounds: number[]): number[] { + const ans: number[] = []; + const m = rounds.length - 1; + if (rounds[0] <= rounds[m]) { + for (let i = rounds[0]; i <= rounds[m]; ++i) { + ans.push(i); + } + } else { + for (let i = 1; i <= rounds[m]; ++i) { + ans.push(i); + } + for (let i = rounds[0]; i <= n; ++i) { + ans.push(i); + } + } + return ans; +} diff --git a/solution/1500-1599/1561.Maximum Number of Coins You Can Get/README.md b/solution/1500-1599/1561.Maximum Number of Coins You Can Get/README.md index 4addb84130633..1ce268e16b21c 100644 --- a/solution/1500-1599/1561.Maximum Number of Coins You Can Get/README.md +++ b/solution/1500-1599/1561.Maximum Number of Coins You Can Get/README.md @@ -76,9 +76,11 @@ tags: -### 方法一：贪心 +### 方法一：贪心 + 排序 -Bob 取走最小的 1/3，剩余的硬币堆由 Alice 和我按硬币数从高到低依次取走每一堆。 +为了让我们获得的硬币数量最多，我们可以贪心地让 Bob 拿走最少的 $n$ 堆硬币。我们每次先让 Alice 拿走最多的一堆硬币，然后让我们拿走第二多的一堆硬币，依次循环，直到没有硬币可拿。 + +时间复杂度 $O(n \times \log n)$，空间复杂度 $O(\log n)$。其中 $n$ 是硬币堆数。 @@ -88,18 +90,17 @@ Bob 取走最小的 1/3，剩余的硬币堆由 Alice 和我按硬币数从高 class Solution: def maxCoins(self, piles: List[int]) -> int: piles.sort() - return sum(piles[-2 : len(piles) // 3 - 1 : -2]) + return sum(piles[len(piles) // 3 :][::2]) ``` #### Java ```java class Solution { - public int maxCoins(int[] piles) { Arrays.sort(piles); int ans = 0; - for (int i = piles.length - 2; i >= piles.length / 3; i -= 2) { + for (int i = piles.length / 3; i < piles.length; i += 2) { ans += piles[i]; } return ans; @@ -113,9 +114,11 @@ class Solution { class Solution { public: int maxCoins(vector & piles) { - sort(piles.begin(), piles.end()); + ranges::sort(piles); int ans = 0; - for (int i = piles.size() - 2; i >= (int) piles.size() / 3; i -= 2) ans += piles[i]; + for (int i = piles.size() / 3; i < piles.size(); i += 2) { + ans += piles[i]; + } return ans; } }; @@ -124,13 +127,12 @@ public: #### Go ```go -func maxCoins(piles []int) int { +func maxCoins(piles []int) (ans int) { sort.Ints(piles) - ans, n := 0, len(piles) - for i := n - 2; i >= n/3; i -= 2 { + for i := len(piles) / 3; i < len(piles); i += 2 { ans += piles[i] } - return ans + return } ``` @@ -139,10 +141,9 @@ func maxCoins(piles []int) int { ```ts function maxCoins(piles: number[]): number { piles.sort((a, b) => a - b); - const n = piles.length; let ans = 0; - for (let i = 1; i <= Math.floor(n / 3); i++) { - ans += piles[n - 2 * i]; + for (let i = piles.length / 3; i < piles.length; i += 2) { + ans += piles[i]; } return ans; } @@ -154,10 +155,9 @@ function maxCoins(piles: number[]): number { impl Solution { pub fn max_coins(mut piles: Vec ) -> i32 { piles.sort(); - let n = piles.len(); let mut ans = 0; - for i in 1..=n / 3 { - ans += piles[n - 2 * i]; + for i in (piles.len() / 3..piles.len()).step_by(2) { + ans += piles[i]; } ans } @@ -167,16 +167,16 @@ impl Solution { #### C ```c -int cmp(const void* a, const void* b) { - return *(int*) a - *(int*) b; +int compare(const void* a, const void* b) { + return (*(int*) a - *(int*) b); } int maxCoins(int* piles, int pilesSize) { - qsort(piles, pilesSize, sizeof(int), cmp); + qsort(piles, pilesSize, sizeof(int), compare); int ans = 0; - for (int i = 1; i <= pilesSize / 3; i++) { - ans += piles[pilesSize - 2 * i]; - }; + for (int i = pilesSize / 3; i < pilesSize; i += 2) { + ans += piles[i]; + } return ans; } ``` diff --git a/solution/1500-1599/1561.Maximum Number of Coins You Can Get/README_EN.md b/solution/1500-1599/1561.Maximum Number of Coins You Can Get/README_EN.md index cdae8d6f3af99..f84cd5b2dfd4e 100644 --- a/solution/1500-1599/1561.Maximum Number of Coins You Can Get/README_EN.md +++ b/solution/1500-1599/1561.Maximum Number of Coins You Can Get/README_EN.md @@ -77,7 +77,11 @@ On the other hand if we choose this arrangement (1, 2, 8), (2, -### Solution 1 +### Solution 1: Greedy + Sorting + +To maximize the number of coins we get, we can greedily let Bob take the smallest $n$ piles of coins. Each time, we let Alice take the largest pile of coins, then we take the second largest pile of coins, and so on, until there are no more coins to take. + +The time complexity is $O(n \times \log n)$, and the space complexity is $O(\log n)$. Here, $n$ is the number of piles of coins. @@ -87,18 +91,17 @@ On the other hand if we choose this arrangement (1, 2, 8), (2, class Solution: def maxCoins(self, piles: List[int]) -> int: piles.sort() - return sum(piles[-2 : len(piles) // 3 - 1 : -2]) + return sum(piles[len(piles) // 3 :][::2]) ``` #### Java ```java class Solution { - public int maxCoins(int[] piles) { Arrays.sort(piles); int ans = 0; - for (int i = piles.length - 2; i >= piles.length / 3; i -= 2) { + for (int i = piles.length / 3; i < piles.length; i += 2) { ans += piles[i]; } return ans; @@ -112,9 +115,11 @@ class Solution { class Solution { public: int maxCoins(vector & piles) { - sort(piles.begin(), piles.end()); + ranges::sort(piles); int ans = 0; - for (int i = piles.size() - 2; i >= (int) piles.size() / 3; i -= 2) ans += piles[i]; + for (int i = piles.size() / 3; i < piles.size(); i += 2) { + ans += piles[i]; + } return ans; } }; @@ -123,13 +128,12 @@ public: #### Go ```go -func maxCoins(piles []int) int { +func maxCoins(piles []int) (ans int) { sort.Ints(piles) - ans, n := 0, len(piles) - for i := n - 2; i >= n/3; i -= 2 { + for i := len(piles) / 3; i < len(piles); i += 2 { ans += piles[i] } - return ans + return } ``` @@ -138,10 +142,9 @@ func maxCoins(piles []int) int { ```ts function maxCoins(piles: number[]): number { piles.sort((a, b) => a - b); - const n = piles.length; let ans = 0; - for (let i = 1; i <= Math.floor(n / 3); i++) { - ans += piles[n - 2 * i]; + for (let i = piles.length / 3; i < piles.length; i += 2) { + ans += piles[i]; } return ans; } @@ -153,10 +156,9 @@ function maxCoins(piles: number[]): number { impl Solution { pub fn max_coins(mut piles: Vec ) -> i32 { piles.sort(); - let n = piles.len(); let mut ans = 0; - for i in 1..=n / 3 { - ans += piles[n - 2 * i]; + for i in (piles.len() / 3..piles.len()).step_by(2) { + ans += piles[i]; } ans } @@ -166,16 +168,16 @@ impl Solution { #### C ```c -int cmp(const void* a, const void* b) { - return *(int*) a - *(int*) b; +int compare(const void* a, const void* b) { + return (*(int*) a - *(int*) b); } int maxCoins(int* piles, int pilesSize) { - qsort(piles, pilesSize, sizeof(int), cmp); + qsort(piles, pilesSize, sizeof(int), compare); int ans = 0; - for (int i = 1; i <= pilesSize / 3; i++) { - ans += piles[pilesSize - 2 * i]; - }; + for (int i = pilesSize / 3; i < pilesSize; i += 2) { + ans += piles[i]; + } return ans; } ``` diff --git a/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.c b/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.c index 03c4ca746fd4f..a8f6df9a259f3 100644 --- a/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.c +++ b/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.c @@ -1,12 +1,12 @@ -int cmp(const void* a, const void* b) { - return *(int*) a - *(int*) b; +int compare(const void* a, const void* b) { + return (*(int*) a - *(int*) b); } int maxCoins(int* piles, int pilesSize) { - qsort(piles, pilesSize, sizeof(int), cmp); + qsort(piles, pilesSize, sizeof(int), compare); int ans = 0; - for (int i = 1; i <= pilesSize / 3; i++) { - ans += piles[pilesSize - 2 * i]; - }; + for (int i = pilesSize / 3; i < pilesSize; i += 2) { + ans += piles[i]; + } return ans; -} \ No newline at end of file +} diff --git a/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.cpp b/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.cpp index 4da1c57716f10..ea3b3ba6fee8a 100644 --- a/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.cpp +++ b/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.cpp @@ -1,9 +1,11 @@ class Solution { public: int maxCoins(vector & piles) { - sort(piles.begin(), piles.end()); + ranges::sort(piles); int ans = 0; - for (int i = piles.size() - 2; i >= (int) piles.size() / 3; i -= 2) ans += piles[i]; + for (int i = piles.size() / 3; i < piles.size(); i += 2) { + ans += piles[i]; + } return ans; } -}; \ No newline at end of file +}; diff --git a/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.go b/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.go index f6b94a1c22a26..3afe054b26b13 100644 --- a/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.go +++ b/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.go @@ -1,8 +1,7 @@ -func maxCoins(piles []int) int { +func maxCoins(piles []int) (ans int) { sort.Ints(piles) - ans, n := 0, len(piles) - for i := n - 2; i >= n/3; i -= 2 { + for i := len(piles) / 3; i < len(piles); i += 2 { ans += piles[i] } - return ans -} \ No newline at end of file + return +} diff --git a/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.java b/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.java index 37427886c5322..66674d9378a62 100644 --- a/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.java +++ b/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.java @@ -1,11 +1,10 @@ class Solution { - public int maxCoins(int[] piles) { Arrays.sort(piles); int ans = 0; - for (int i = piles.length - 2; i >= piles.length / 3; i -= 2) { + for (int i = piles.length / 3; i < piles.length; i += 2) { ans += piles[i]; } return ans; } -} \ No newline at end of file +} diff --git a/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.py b/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.py index 4acd66f1aba0c..c8113dec93482 100644 --- a/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.py +++ b/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.py @@ -1,4 +1,4 @@ class Solution: def maxCoins(self, piles: List[int]) -> int: piles.sort() - return sum(piles[-2 : len(piles) // 3 - 1 : -2]) + return sum(piles[len(piles) // 3 :][::2]) diff --git a/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.rs b/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.rs index cca8213b54801..fd259f82e37b7 100644 --- a/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.rs +++ b/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.rs @@ -1,10 +1,9 @@ impl Solution { pub fn max_coins(mut piles: Vec ) -> i32 { piles.sort(); - let n = piles.len(); let mut ans = 0; - for i in 1..=n / 3 { - ans += piles[n - 2 * i]; + for i in (piles.len() / 3..piles.len()).step_by(2) { + ans += piles[i]; } ans } diff --git a/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.ts b/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.ts index e1b929cfc6e28..3149a184879c3 100644 --- a/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.ts +++ b/solution/1500-1599/1561.Maximum Number of Coins You Can Get/Solution.ts @@ -1,9 +1,8 @@ function maxCoins(piles: number[]): number { piles.sort((a, b) => a - b); - const n = piles.length; let ans = 0; - for (let i = 1; i <= Math.floor(n / 3); i++) { - ans += piles[n - 2 * i]; + for (let i = piles.length / 3; i < piles.length; i += 2) { + ans += piles[i]; } return ans; } diff --git a/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/README.md b/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/README.md index d097b9262ad02..88c1200b05767 100644 --- a/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/README.md +++ b/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/README.md @@ -79,11 +79,15 @@ tags: -### 方法一：枚举 +### 方法一：一次遍历 -枚举数组的左端点 `i`，判断是否存在一个 `i`，满足对于任意 `j∈[0, m * k)`，`arr[i + j] == arr[i + (j % m)]`。存在则返回 `true`，否则返回 `false`。 +首先，如果数组的长度小于 $m \times k$，那么肯定不存在长度为 $m$ 且至少重复 $k$ 次的模式，直接返回 $\textit{false}$。 -时间复杂度 $O((n-m\times k)\times m \times k)$。 +接下来，我们定义一个变量 $\textit{cnt}$ 来记录当前连续重复的次数，如果数组存在连续的 $(k - 1) \times m$ 个元素 $a_i$，使得 $a_i = a_{i - m}$，那么我们就找到了一个长度为 $m$ 且至少重复 $k$ 次的模式，返回 $\textit{true}$。否则，我们将 $\textit{cnt}$ 置为 $0$，继续遍历数组。 + +最后，如果遍历完数组都没有找到符合条件的模式，返回 $\textit{false}$。 + +时间复杂度 $O(n)$，其中 $n$ 是数组的长度。空间复杂度 $O(1)$。 @@ -92,15 +96,16 @@ tags: ```python class Solution: def containsPattern(self, arr: List[int], m: int, k: int) -> bool: - n = len(arr) - for i in range(n - m * k + 1): - j = 0 - while j < m * k: - if arr[i + j] != arr[i + (j % m)]: - break - j += 1 - if j == m * k: - return True + if len(arr) < m * k: + return False + cnt, target = 0, (k - 1) * m + for i in range(m, len(arr)): + if arr[i] == arr[i - m]: + cnt += 1 + if cnt == target: + return True + else: + cnt = 0 return False ``` @@ -109,16 +114,17 @@ class Solution: ```java class Solution { public boolean containsPattern(int[] arr, int m, int k) { - int n = arr.length; - for (int i = 0; i <= n - m * k; ++i) { - int j = 0; - for (; j < m * k; ++j) { - if (arr[i + j] != arr[i + (j % m)]) { - break; + if (arr.length < m * k) { + return false; + } + int cnt = 0, target = (k - 1) * m; + for (int i = m; i < arr.length; ++i) { + if (arr[i] == arr[i - m]) { + if (++cnt == target) { + return true; } - } - if (j == m * k) { - return true; + } else { + cnt = 0; } } return false; @@ -132,16 +138,17 @@ class Solution { class Solution { public: bool containsPattern(vector & arr, int m, int k) { - int n = arr.size(); - for (int i = 0; i <= n - m * k; ++i) { - int j = 0; - for (; j < m * k; ++j) { - if (arr[i + j] != arr[i + (j % m)]) { - break; + if (arr.size() < m * k) { + return false; + } + int cnt = 0, target = (k - 1) * m; + for (int i = m; i < arr.size(); ++i) { + if (arr[i] == arr[i - m]) { + if (++cnt == target) { + return true; } - } - if (j == m * k) { - return true; + } else { + cnt = 0; } } return false; @@ -153,16 +160,15 @@ public: ```go func containsPattern(arr []int, m int, k int) bool { - n := len(arr) - for i := 0; i <= n-m*k; i++ { - j := 0 - for ; j < m*k; j++ { - if arr[i+j] != arr[i+(j%m)] { - break + cnt, target := 0, (k-1)*m + for i := m; i < len(arr); i++ { + if arr[i] == arr[i-m] { + cnt++ + if cnt == target { + return true } - } - if j == m*k { - return true + } else { + cnt = 0 } } return false @@ -173,16 +179,18 @@ func containsPattern(arr []int, m int, k int) bool { ```ts function containsPattern(arr: number[], m: number, k: number): boolean { - const n = arr.length; - for (let i = 0; i <= n - m * k; ++i) { - let j = 0; - for (; j < m * k; ++j) { - if (arr[i + j] != arr[i + (j % m)]) { - break; + if (arr.length < m * k) { + return false; + } + const target = (k - 1) * m; + let cnt = 0; + for (let i = m; i < arr.length; ++i) { + if (arr[i] === arr[i - m]) { + if (++cnt === target) { + return true; } - } - if (j == m * k) { - return true; + } else { + cnt = 0; } } return false; diff --git a/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/README_EN.md b/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/README_EN.md index 22217fd4c41ab..7cd0cde5d5890 100644 --- a/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/README_EN.md +++ b/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/README_EN.md @@ -66,7 +66,15 @@ tags: -### Solution 1 +### Solution 1: Single Traversal + +First, if the length of the array is less than $m \times k$, then there is definitely no pattern of length $m$ that repeats at least $k$ times, so we directly return $\textit{false}$. + +Next, we define a variable $\textit{cnt}$ to record the current count of consecutive repetitions. If there are $(k - 1) \times m$ consecutive elements $a_i$ in the array such that $a_i = a_{i - m}$, then we have found a pattern of length $m$ that repeats at least $k$ times, and we return $\textit{true}$. Otherwise, we reset $\textit{cnt}$ to $0$ and continue traversing the array. + +Finally, if we finish traversing the array without finding a pattern that meets the conditions, we return $\textit{false}$. + +The time complexity is $O(n)$, where $n$ is the length of the array. The space complexity is $O(1)$. @@ -75,15 +83,16 @@ tags: ```python class Solution: def containsPattern(self, arr: List[int], m: int, k: int) -> bool: - n = len(arr) - for i in range(n - m * k + 1): - j = 0 - while j < m * k: - if arr[i + j] != arr[i + (j % m)]: - break - j += 1 - if j == m * k: - return True + if len(arr) < m * k: + return False + cnt, target = 0, (k - 1) * m + for i in range(m, len(arr)): + if arr[i] == arr[i - m]: + cnt += 1 + if cnt == target: + return True + else: + cnt = 0 return False ``` @@ -92,16 +101,17 @@ class Solution: ```java class Solution { public boolean containsPattern(int[] arr, int m, int k) { - int n = arr.length; - for (int i = 0; i <= n - m * k; ++i) { - int j = 0; - for (; j < m * k; ++j) { - if (arr[i + j] != arr[i + (j % m)]) { - break; + if (arr.length < m * k) { + return false; + } + int cnt = 0, target = (k - 1) * m; + for (int i = m; i < arr.length; ++i) { + if (arr[i] == arr[i - m]) { + if (++cnt == target) { + return true; } - } - if (j == m * k) { - return true; + } else { + cnt = 0; } } return false; @@ -115,16 +125,17 @@ class Solution { class Solution { public: bool containsPattern(vector & arr, int m, int k) { - int n = arr.size(); - for (int i = 0; i <= n - m * k; ++i) { - int j = 0; - for (; j < m * k; ++j) { - if (arr[i + j] != arr[i + (j % m)]) { - break; + if (arr.size() < m * k) { + return false; + } + int cnt = 0, target = (k - 1) * m; + for (int i = m; i < arr.size(); ++i) { + if (arr[i] == arr[i - m]) { + if (++cnt == target) { + return true; } - } - if (j == m * k) { - return true; + } else { + cnt = 0; } } return false; @@ -136,16 +147,15 @@ public: ```go func containsPattern(arr []int, m int, k int) bool { - n := len(arr) - for i := 0; i <= n-m*k; i++ { - j := 0 - for ; j < m*k; j++ { - if arr[i+j] != arr[i+(j%m)] { - break + cnt, target := 0, (k-1)*m + for i := m; i < len(arr); i++ { + if arr[i] == arr[i-m] { + cnt++ + if cnt == target { + return true } - } - if j == m*k { - return true + } else { + cnt = 0 } } return false @@ -156,16 +166,18 @@ func containsPattern(arr []int, m int, k int) bool { ```ts function containsPattern(arr: number[], m: number, k: number): boolean { - const n = arr.length; - for (let i = 0; i <= n - m * k; ++i) { - let j = 0; - for (; j < m * k; ++j) { - if (arr[i + j] != arr[i + (j % m)]) { - break; + if (arr.length < m * k) { + return false; + } + const target = (k - 1) * m; + let cnt = 0; + for (let i = m; i < arr.length; ++i) { + if (arr[i] === arr[i - m]) { + if (++cnt === target) { + return true; } - } - if (j == m * k) { - return true; + } else { + cnt = 0; } } return false; diff --git a/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.cpp b/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.cpp index 1094f7ab350ed..663a377a29913 100644 --- a/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.cpp +++ b/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.cpp @@ -1,18 +1,19 @@ class Solution { public: bool containsPattern(vector & arr, int m, int k) { - int n = arr.size(); - for (int i = 0; i <= n - m * k; ++i) { - int j = 0; - for (; j < m * k; ++j) { - if (arr[i + j] != arr[i + (j % m)]) { - break; + if (arr.size() < m * k) { + return false; + } + int cnt = 0, target = (k - 1) * m; + for (int i = m; i < arr.size(); ++i) { + if (arr[i] == arr[i - m]) { + if (++cnt == target) { + return true; } - } - if (j == m * k) { - return true; + } else { + cnt = 0; } } return false; } -}; \ No newline at end of file +}; diff --git a/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.go b/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.go index 1f5199fd00aad..f6713f12c2fa0 100644 --- a/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.go +++ b/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.go @@ -1,15 +1,14 @@ func containsPattern(arr []int, m int, k int) bool { - n := len(arr) - for i := 0; i <= n-m*k; i++ { - j := 0 - for ; j < m*k; j++ { - if arr[i+j] != arr[i+(j%m)] { - break + cnt, target := 0, (k-1)*m + for i := m; i < len(arr); i++ { + if arr[i] == arr[i-m] { + cnt++ + if cnt == target { + return true } - } - if j == m*k { - return true + } else { + cnt = 0 } } return false -} \ No newline at end of file +} diff --git a/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.java b/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.java index e5f17fbb08c0b..6364d5dba9abd 100644 --- a/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.java +++ b/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.java @@ -1,17 +1,18 @@ class Solution { public boolean containsPattern(int[] arr, int m, int k) { - int n = arr.length; - for (int i = 0; i <= n - m * k; ++i) { - int j = 0; - for (; j < m * k; ++j) { - if (arr[i + j] != arr[i + (j % m)]) { - break; + if (arr.length < m * k) { + return false; + } + int cnt = 0, target = (k - 1) * m; + for (int i = m; i < arr.length; ++i) { + if (arr[i] == arr[i - m]) { + if (++cnt == target) { + return true; } - } - if (j == m * k) { - return true; + } else { + cnt = 0; } } return false; } -} \ No newline at end of file +} diff --git a/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.py b/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.py index 20beb1a6d26ad..6921486ca9df4 100644 --- a/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.py +++ b/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.py @@ -1,12 +1,13 @@ class Solution: def containsPattern(self, arr: List[int], m: int, k: int) -> bool: - n = len(arr) - for i in range(n - m * k + 1): - j = 0 - while j < m * k: - if arr[i + j] != arr[i + (j % m)]: - break - j += 1 - if j == m * k: - return True + if len(arr) < m * k: + return False + cnt, target = 0, (k - 1) * m + for i in range(m, len(arr)): + if arr[i] == arr[i - m]: + cnt += 1 + if cnt == target: + return True + else: + cnt = 0 return False diff --git a/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.ts b/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.ts index 98c1eac1056bc..affe2719682cb 100644 --- a/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.ts +++ b/solution/1500-1599/1566.Detect Pattern of Length M Repeated K or More Times/Solution.ts @@ -1,14 +1,16 @@ function containsPattern(arr: number[], m: number, k: number): boolean { - const n = arr.length; - for (let i = 0; i <= n - m * k; ++i) { - let j = 0; - for (; j < m * k; ++j) { - if (arr[i + j] != arr[i + (j % m)]) { - break; + if (arr.length < m * k) { + return false; + } + const target = (k - 1) * m; + let cnt = 0; + for (let i = m; i < arr.length; ++i) { + if (arr[i] === arr[i - m]) { + if (++cnt === target) { + return true; } - } - if (j == m * k) { - return true; + } else { + cnt = 0; } } return false; diff --git a/solution/1600-1699/1666.Change the Root of a Binary Tree/README.md b/solution/1600-1699/1666.Change the Root of a Binary Tree/README.md index 5649a38b4105f..7cda4054fa74d 100644 --- a/solution/1600-1699/1666.Change the Root of a Binary Tree/README.md +++ b/solution/1600-1699/1666.Change the Root of a Binary Tree/README.md @@ -18,42 +18,44 @@ tags: - 给定一棵二叉树的根节点
+root和一个叶节点leaf，更改二叉树，使得leaf为新的根节点。给定一棵二叉树的根节点
-root和一个叶节点leaf，更改二叉树，使得leaf为新的根节点。你可以按照下列步骤修改从
+leaf到root的路径中除root外的每个节点cur：你可以按照下列步骤修改从
leaf到root的路径中除root外的每个节点cur：-
- 如果
-cur有左子节点，则该子节点变为cur的右子节点。注意我们保证cur至多有一个子节点。- +
cur的原父节点变为cur的左子节点。- 如果
+cur有左子节点，则该子节点变为cur的右子节点。注意我们保证cur至多有一个子节点。cur的原父节点变为cur的左子节点。返回修改后新树的根节点。
-注意：确保你的答案在操作后正确地设定了
+Node.parent（父节点）指针，否则会被判为错误答案。注意：确保你的答案在操作后正确地设定了
-Node.parent（父节点）指针，否则会被判为错误答案。+
示例 1:
--
输入: root = [3,5,1,6,2,0,8,null,null,7,4], leaf = 7 ++
+输入: root = [3,5,1,6,2,0,8,null,null,7,4], leaf = 7 输出: [7,2,null,5,4,3,6,null,null,null,1,null,null,0,8]示例 2:
-输入: root = [3,5,1,6,2,0,8,null,null,7,4], leaf = 0 ++输入: root = [3,5,1,6,2,0,8,null,null,7,4], leaf = 0 输出: [0,1,null,3,8,5,null,null,null,6,2,null,null,7,4]-+
提示:
-
diff --git a/solution/1600-1699/1666.Change the Root of a Binary Tree/README_EN.md b/solution/1600-1699/1666.Change the Root of a Binary Tree/README_EN.md index 9cf85b2f1ad9b..25843aab5c5a1 100644 --- a/solution/1600-1699/1666.Change the Root of a Binary Tree/README_EN.md +++ b/solution/1600-1699/1666.Change the Root of a Binary Tree/README_EN.md @@ -33,7 +33,7 @@ tags:- 树中节点的个数在范围
+[2, 100]内。- 树中节点的个数在范围
[2, 100]内。- -
-109 <= Node.val <= 109- 所有的
-Node.val都是唯一的。- +
leaf存在于树中。- 所有的
+Node.val都是唯一的。leaf存在于树中。
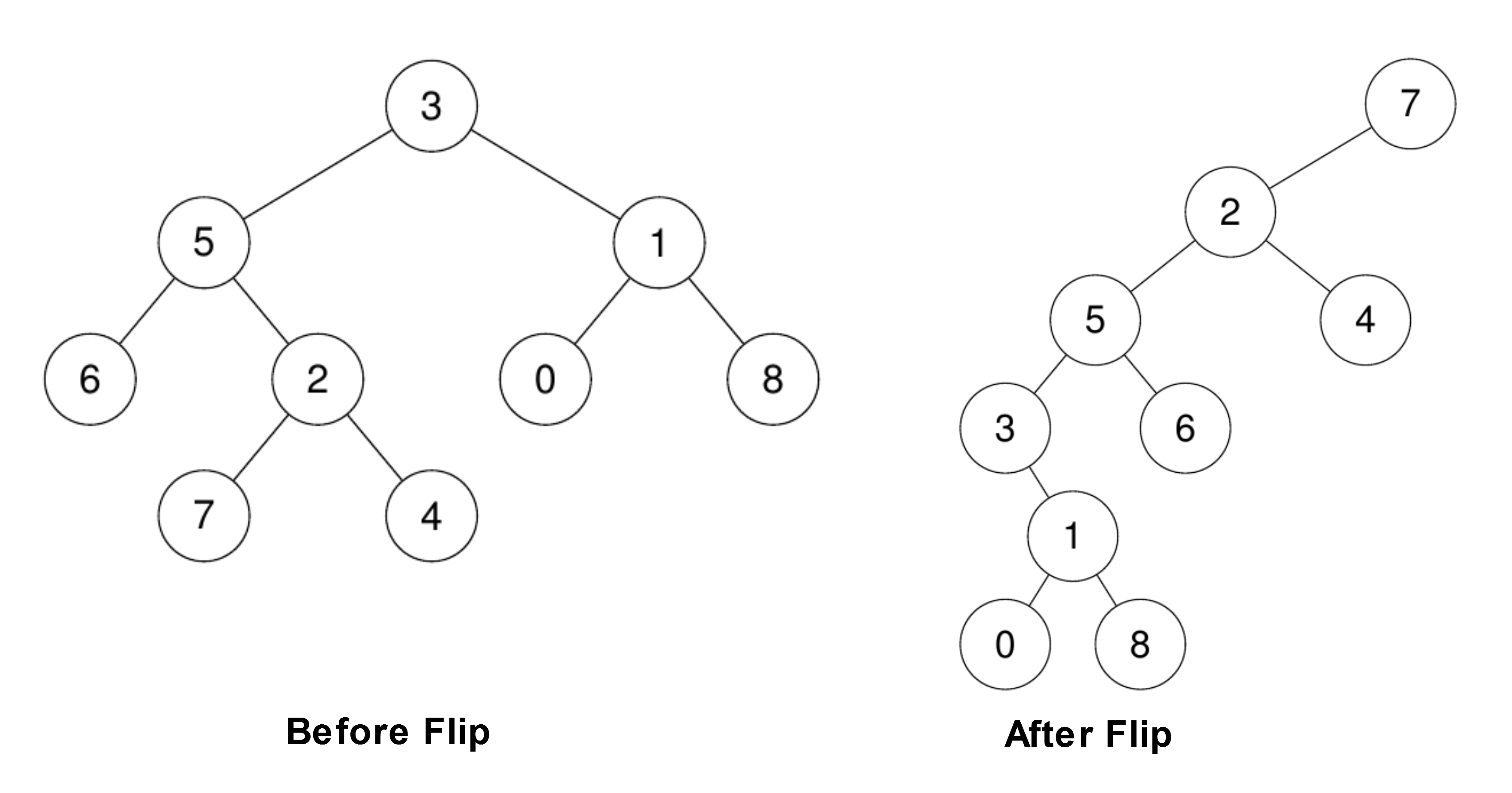
Example 1:
-
Input: root = [3,5,1,6,2,0,8,null,null,7,4], leaf = 7 Output: [7,2,null,5,4,3,6,null,null,null,1,null,null,0,8] diff --git a/solution/1600-1699/1666.Change the Root of a Binary Tree/images/1727138189-YtDgTf-image.png b/solution/1600-1699/1666.Change the Root of a Binary Tree/images/1727138189-YtDgTf-image.png new file mode 100644 index 0000000000000..3d1a9d119c8d7 Binary files /dev/null and b/solution/1600-1699/1666.Change the Root of a Binary Tree/images/1727138189-YtDgTf-image.png differ diff --git a/solution/1600-1699/1666.Change the Root of a Binary Tree/images/bt_image_1.png b/solution/1600-1699/1666.Change the Root of a Binary Tree/images/bt_image_1.png new file mode 100644 index 0000000000000..f00577bd6814e Binary files /dev/null and b/solution/1600-1699/1666.Change the Root of a Binary Tree/images/bt_image_1.png differ diff --git a/solution/1600-1699/1666.Change the Root of a Binary Tree/images/fliptree.png b/solution/1600-1699/1666.Change the Root of a Binary Tree/images/fliptree.png deleted file mode 100644 index 4c9ea468f2dae..0000000000000 Binary files a/solution/1600-1699/1666.Change the Root of a Binary Tree/images/fliptree.png and /dev/null differ diff --git a/solution/1800-1899/1858.Longest Word With All Prefixes/README_EN.md b/solution/1800-1899/1858.Longest Word With All Prefixes/README_EN.md index 05dd57c29e9c6..c9983247f32f8 100644 --- a/solution/1800-1899/1858.Longest Word With All Prefixes/README_EN.md +++ b/solution/1800-1899/1858.Longest Word With All Prefixes/README_EN.md @@ -20,63 +20,44 @@ tags:Given an array of strings
words, find the longest string inwordssuch that every prefix of it is also inwords.- -
- For example, let
- +words = ["a", "app", "ap"]. The string"app"has prefixes"ap"and"a", all of which are inwords.- For example, let
words = ["a", "app", "ap"]. The string"app"has prefixes"ap"and"a", all of which are inwords.Return the string described above. If there is more than one string with the same length, return the lexicographically smallest one, and if no string exists, return
"".-
Example 1:
- Input: words = ["k","ki","kir","kira", "kiran"] - Output: "kiran" - Explanation: "kiran" has prefixes "kira", "kir", "ki", and "k", and all of them appear in words. -Example 2:
- Input: words = ["a", "banana", "app", "appl", "ap", "apply", "apple"] - Output: "apple" - Explanation: Both "apple" and "apply" have all their prefixes in words. - However, "apple" is lexicographically smaller, so we return that. -Example 3:
- Input: words = ["abc", "bc", "ab", "qwe"] - Output: "" --
Constraints:
- -
diff --git a/solution/2000-2099/2073.Time Needed to Buy Tickets/README.md b/solution/2000-2099/2073.Time Needed to Buy Tickets/README.md index 270790dde6a7e..ab03033cb9a4a 100644 --- a/solution/2000-2099/2073.Time Needed to Buy Tickets/README.md +++ b/solution/2000-2099/2073.Time Needed to Buy Tickets/README.md @@ -32,23 +32,40 @@ tags:- - -
1 <= words.length <= 105- - -
1 <= words[i].length <= 105- - +
1 <= sum(words[i].length) <= 105- +
1 <= words.length <= 105- +
1 <= words[i].length <= 105- +
1 <= sum(words[i].length) <= 105words[i]consists only of lowercase English letters.示例 1：
-输入：tickets = [2,3,2], k = 2 -输出：6 -解释： -- 第一轮，队伍中的每个人都买到一张票，队伍变为 [1, 2, 1] 。 -- 第二轮，队伍中的每个都又都买到一张票，队伍变为 [0, 1, 0] 。 -位置 2 的人成功买到 2 张票，用掉 3 + 3 = 6 秒。 -+输入：tickets = [2,3,2], k = 2+ +输出：6+ +解释：+ ++ ++
+ +- 队伍一开始为 [2,3,2]，第 k 个人以下划线标识。
+- 在最前面的人买完票后，队伍在第 1 秒变成 [3,2,1]。
+- 继续这个过程，队伍在第 2 秒变为[2,1,2]。
+- 继续这个过程，队伍在第 3 秒变为[1,2,1]。
+- 继续这个过程，队伍在第 4 秒变为[2,1]。
+- 继续这个过程，队伍在第 5 秒变为[1,1]。
+- 继续这个过程，队伍在第 6 秒变为[1]。第 k 个人完成买票，所以返回 6。
+示例 2：
-输入：tickets = [5,1,1,1], k = 0 -输出：8 -解释： -- 第一轮，队伍中的每个人都买到一张票，队伍变为 [4, 0, 0, 0] 。 -- 接下来的 4 轮，只有位置 0 的人在买票。 -位置 0 的人成功买到 5 张票，用掉 4 + 1 + 1 + 1 + 1 = 8 秒。 -+输入：tickets = [5,1,1,1], k = 0+ +输出：8+ +解释：+ ++
- 队伍一开始为 [5,1,1,1]，第 k 个人以下划线标识。
+- 在最前面的人买完票后，队伍在第 1 秒变成 [1,1,1,4]。
+- 继续这个过程 3 秒，队伍在第 4 秒变为[4]。
+- 继续这个过程 4 秒，队伍在第 8 秒变为[]。第 k 个人完成买票，所以返回 8。
+diff --git a/solution/2000-2099/2073.Time Needed to Buy Tickets/README_EN.md b/solution/2000-2099/2073.Time Needed to Buy Tickets/README_EN.md index 1a6e414d287fe..dbbf02f284c20 100644 --- a/solution/2000-2099/2073.Time Needed to Buy Tickets/README_EN.md +++ b/solution/2000-2099/2073.Time Needed to Buy Tickets/README_EN.md @@ -26,30 +26,45 @@ tags:
Each person takes exactly 1 second to buy a ticket. A person can only buy 1 ticket at a time and has to go back to the end of the line (which happens instantaneously) in order to buy more tickets. If a person does not have any tickets left to buy, the person will leave the line.
-Return the time taken for the person at position
+k(0-indexed) to finish buying tickets.Return the time taken for the person initially at position k (0-indexed) to finish buying tickets.
Example 1:
--Input: tickets = [2,3,2], k = 2 -Output: 6 -Explanation: -- In the first pass, everyone in the line buys a ticket and the line becomes [1, 2, 1]. -- In the second pass, everyone in the line buys a ticket and the line becomes [0, 1, 0]. -The person at position 2 has successfully bought 2 tickets and it took 3 + 3 = 6 seconds. -++Input: tickets = [2,3,2], k = 2
+ +Output: 6
+ +Explanation:
+ ++
+- The queue starts as [2,3,2], where the kth person is underlined.
+- After the person at the front has bought a ticket, the queue becomes [3,2,1] at 1 second.
+- Continuing this process, the queue becomes [2,1,2] at 2 seconds.
+- Continuing this process, the queue becomes [1,2,1] at 3 seconds.
+- Continuing this process, the queue becomes [2,1] at 4 seconds. Note: the person at the front left the queue.
+- Continuing this process, the queue becomes [1,1] at 5 seconds.
+- Continuing this process, the queue becomes [1] at 6 seconds. The kth person has bought all their tickets, so return 6.
+Example 2:
--Input: tickets = [5,1,1,1], k = 0 -Output: 8 -Explanation: -- In the first pass, everyone in the line buys a ticket and the line becomes [4, 0, 0, 0]. -- In the next 4 passes, only the person in position 0 is buying tickets. -The person at position 0 has successfully bought 5 tickets and it took 4 + 1 + 1 + 1 + 1 = 8 seconds. -++Input: tickets = [5,1,1,1], k = 0
+ +Output: 8
+ +Explanation:
+ ++
+- The queue starts as [5,1,1,1], where the kth person is underlined.
+- After the person at the front has bought a ticket, the queue becomes [1,1,1,4] at 1 second.
+- Continuing this process for 3 seconds, the queue becomes [4] at 4 seconds.
+- Continuing this process for 4 seconds, the queue becomes [] at 8 seconds. The kth person has bought all their tickets, so return 8.
+
Constraints:
diff --git a/solution/2300-2399/2306.Naming a Company/README.md b/solution/2300-2399/2306.Naming a Company/README.md index c56b0c39063f3..8df5ab83fb3c1 100644 --- a/solution/2300-2399/2306.Naming a Company/README.md +++ b/solution/2300-2399/2306.Naming a Company/README.md @@ -80,15 +80,15 @@ tags: ### 方法一：枚举计数 -我们定义 $f[i][j]$ 表示 $ideas$ 中以第 $i$ 个字母开头，替换为第 $j$ 个字母后，不在 $ideas$ 中的字符串的个数。初始时 $f[i][j] = 0$。另外，用一个哈希表 $s$ 记录 $ideas$ 中的字符串，方便我们开快速判断某个字符串是否在 $ideas$ 中。 +我们定义 $f[i][j]$ 表示 $\textit{ideas}$ 中以第 $i$ 个字母开头，替换为第 $j$ 个字母后，不在 $\textit{ideas}$ 中的字符串的个数。初始时 $f[i][j] = 0$。另外，用一个哈希表 $s$ 记录 $\textit{ideas}$ 中的字符串，方便我们快速判断某个字符串是否在 $\textit{ideas}$ 中。 -接下来，我们遍历 $ideas$ 中字符串，对于当前遍历到的字符串 $v$，我们枚举替换后的第一个字母 $j$，如果 $v$ 替换后的字符串不在 $ideas$ 中，那么我们就更新 $f[i][j] = f[i][j] + 1$。 +接下来，我们遍历 $\textit{ideas}$ 中字符串，对于当前遍历到的字符串 $v$，我们枚举替换后的第一个字母 $j$，如果 $v$ 替换后的字符串不在 $\textit{ideas}$ 中，那么我们就更新 $f[i][j] = f[i][j] + 1$。 -最后，我们再次遍历 $ideas$ 中字符串，对于当前遍历到的字符串 $v$，我们枚举替换后的第一个字母 $j$，如果 $v$ 替换后的字符串不在 $ideas$ 中，那么我们就更新答案 $ans = ans + f[j][i]$。 +最后，我们再次遍历 $\textit{ideas}$ 中字符串，对于当前遍历到的字符串 $v$，我们枚举替换后的第一个字母 $j$，如果 $v$ 替换后的字符串不在 $\textit{ideas}$ 中，那么我们就更新答案 $\textit{ans} = \textit{ans} + f[j][i]$。 -最终答案即为 $ans$。 +最终答案即为 $\textit{ans}$。 -时间复杂度 $O(n \times m \times |\Sigma|)$，空间复杂度 $O(|\Sigma|^2)$。其中 $n$ 和 $m$ 分别是 $ideas$ 中字符串的个数和字符串的最大长度，而 $|\Sigma|$ 是字符串中出现的字符集，本题中 $|\Sigma| \leq 26$。 +时间复杂度 $O(n \times m \times |\Sigma|)$，空间复杂度 $O(|\Sigma|^2)$。其中 $n$ 和 $m$ 分别是 $\textit{ideas}$ 中字符串的个数和字符串的最大长度，而 $|\Sigma|$ 是字符串中出现的字符集，本题中 $|\Sigma| \leq 26$。 @@ -219,39 +219,6 @@ func distinctNames(ideas []string) (ans int64) { } ``` -#### TypeScript - -```ts -function distinctNames(ideas: string[]): number { - const s = new Set(ideas); - const f: number[][] = Array(26) - .fill(0) - .map(() => Array(26).fill(0)); - for (const v of s) { - const i = v.charCodeAt(0) - 'a'.charCodeAt(0); - const t = [...v]; - for (let j = 0; j < 26; ++j) { - t[0] = String.fromCharCode('a'.charCodeAt(0) + j); - if (!s.has(t.join(''))) { - f[i][j]++; - } - } - } - let ans = 0; - for (const v of s) { - const i = v.charCodeAt(0) - 'a'.charCodeAt(0); - const t = [...v]; - for (let j = 0; j < 26; ++j) { - t[0] = String.fromCharCode('a'.charCodeAt(0) + j); - if (!s.has(t.join(''))) { - ans += f[j][i]; - } - } - } - return ans; -} -``` - diff --git a/solution/2300-2399/2306.Naming a Company/README_EN.md b/solution/2300-2399/2306.Naming a Company/README_EN.md index 9d0016530900a..96af6032c5b0c 100644 --- a/solution/2300-2399/2306.Naming a Company/README_EN.md +++ b/solution/2300-2399/2306.Naming a Company/README_EN.md @@ -78,17 +78,17 @@ The following are some examples of invalid selections: -### Solution 1: Enumeration Counting +### Solution 1: Enumeration and Counting -We define $f[i][j]$ to represent the number of strings in $ideas$ that start with the $i$th letter and are not in $ideas$ after being replaced with the $j$th letter. Initially, $f[i][j] = 0$. Additionally, we use a hash table $s$ to record the strings in $ideas$, which allows us to quickly determine whether a string is in $ideas$. +We define $f[i][j]$ to represent the number of strings in $\textit{ideas}$ that start with the $i$-th letter and, when replaced with the $j$-th letter, do not exist in $\textit{ideas}$. Initially, $f[i][j] = 0$. Additionally, we use a hash table $s$ to record the strings in $\textit{ideas}$, allowing us to quickly determine whether a string is in $\textit{ideas}$. -Next, we traverse the strings in $ideas$. For the current string $v$, we enumerate the first letter $j$ after replacement. If the string after $v$ is replaced is not in $ideas$, then we update $f[i][j] = f[i][j] + 1$. +Next, we traverse the strings in $\textit{ideas}$. For the current string $v$, we enumerate the first letter $j$ after replacement. If the string obtained by replacing $v$ is not in $\textit{ideas}$, we update $f[i][j] = f[i][j] + 1$. -Finally, we traverse the strings in $ideas$ again. For the current string $v$, we enumerate the first letter $j$ after replacement. If the string after $v$ is replaced is not in $ideas$, then we update the answer $ans = ans + f[j][i]$. +Finally, we traverse the strings in $\textit{ideas}$ again. For the current string $v$, we enumerate the first letter $j$ after replacement. If the string obtained by replacing $v$ is not in $\textit{ideas}$, we update the answer $\textit{ans} = \textit{ans} + f[j][i]$. -The final answer is $ans$. +The final answer is $\textit{ans}$. -The time complexity is $O(n \times m \times |\Sigma|)$, and the space complexity is $O(|\Sigma|^2)$. Here, $n$ and $m$ are the number of strings in $ideas$ and the maximum length of the strings, respectively, and $|\Sigma|$ is the character set that appears in the string. In this problem, $|\Sigma| \leq 26$. +The time complexity is $O(n \times m \times |\Sigma|)$, and the space complexity is $O(|\Sigma|^2)$. Here, $n$ and $m$ are the number of strings in $\textit{ideas}$ and the maximum length of the strings, respectively, and $|\Sigma|$ is the character set of the strings, with $|\Sigma| \leq 26$ in this problem. @@ -219,39 +219,6 @@ func distinctNames(ideas []string) (ans int64) { } ``` -#### TypeScript - -```ts -function distinctNames(ideas: string[]): number { - const s = new Set(ideas); - const f: number[][] = Array(26) - .fill(0) - .map(() => Array(26).fill(0)); - for (const v of s) { - const i = v.charCodeAt(0) - 'a'.charCodeAt(0); - const t = [...v]; - for (let j = 0; j < 26; ++j) { - t[0] = String.fromCharCode('a'.charCodeAt(0) + j); - if (!s.has(t.join(''))) { - f[i][j]++; - } - } - } - let ans = 0; - for (const v of s) { - const i = v.charCodeAt(0) - 'a'.charCodeAt(0); - const t = [...v]; - for (let j = 0; j < 26; ++j) { - t[0] = String.fromCharCode('a'.charCodeAt(0) + j); - if (!s.has(t.join(''))) { - ans += f[j][i]; - } - } - } - return ans; -} -``` - diff --git a/solution/2300-2399/2306.Naming a Company/Solution.ts b/solution/2300-2399/2306.Naming a Company/Solution.ts deleted file mode 100644 index 3dfe1e5d41b13..0000000000000 --- a/solution/2300-2399/2306.Naming a Company/Solution.ts +++ /dev/null @@ -1,28 +0,0 @@ -function distinctNames(ideas: string[]): number { - const s = new Set(ideas); - const f: number[][] = Array(26) - .fill(0) - .map(() => Array(26).fill(0)); - for (const v of s) { - const i = v.charCodeAt(0) - 'a'.charCodeAt(0); - const t = [...v]; - for (let j = 0; j < 26; ++j) { - t[0] = String.fromCharCode('a'.charCodeAt(0) + j); - if (!s.has(t.join(''))) { - f[i][j]++; - } - } - } - let ans = 0; - for (const v of s) { - const i = v.charCodeAt(0) - 'a'.charCodeAt(0); - const t = [...v]; - for (let j = 0; j < 26; ++j) { - t[0] = String.fromCharCode('a'.charCodeAt(0) + j); - if (!s.has(t.join(''))) { - ans += f[j][i]; - } - } - } - return ans; -} diff --git a/solution/2300-2399/2332.The Latest Time to Catch a Bus/README.md b/solution/2300-2399/2332.The Latest Time to Catch a Bus/README.md index 04d884c429f0a..55709f544df1f 100644 --- a/solution/2300-2399/2332.The Latest Time to Catch a Bus/README.md +++ b/solution/2300-2399/2332.The Latest Time to Catch a Bus/README.md @@ -25,7 +25,7 @@ tags:给你一个整数
-capacity，表示每辆公交车 最多 能容纳的乘客数目。每位乘客都会搭乘下一辆有座位的公交车。如果你在
+y时刻到达，公交在x时刻出发，满足y <= x且公交没有满，那么你可以搭乘这一辆公交。最早 到达的乘客优先上车。每位乘客都会排队搭乘下一辆有座位的公交车。如果你在
y时刻到达，公交在x时刻出发，满足y <= x且公交没有满，那么你可以搭乘这一辆公交。最早 到达的乘客优先上车。返回你可以搭乘公交车的最晚到达公交站时间。你 不能 跟别的乘客同时刻到达。
@@ -35,7 +35,8 @@ tags:示例 1：
-输入：buses = [10,20], passengers = [2,17,18,19], capacity = 2 ++输入：buses = [10,20], passengers = [2,17,18,19], capacity = 2 输出：16 解释： 第 1 辆公交车载着第 1 位乘客。 @@ -44,7 +45,8 @@ tags:示例 2：
-输入：buses = [20,30,10], passengers = [19,13,26,4,25,11,21], capacity = 2 ++输入：buses = [20,30,10], passengers = [19,13,26,4,25,11,21], capacity = 2 输出：20 解释： 第 1 辆公交车载着第 4 位乘客。 diff --git a/solution/2300-2399/2333.Minimum Sum of Squared Difference/README.md b/solution/2300-2399/2333.Minimum Sum of Squared Difference/README.md index 0111eaa0fe786..b8e7f03b18d75 100644 --- a/solution/2300-2399/2333.Minimum Sum of Squared Difference/README.md +++ b/solution/2300-2399/2333.Minimum Sum of Squared Difference/README.md @@ -5,8 +5,9 @@ edit_url: https://github.com/doocs/leetcode/edit/main/solution/2300-2399/2333.Mi rating: 2011 source: 第 82 场双周赛 Q3 tags: + - 贪心 - 数组 - - 数学 + - 二分查找 - 排序 - 堆（优先队列） --- diff --git a/solution/2300-2399/2333.Minimum Sum of Squared Difference/README_EN.md b/solution/2300-2399/2333.Minimum Sum of Squared Difference/README_EN.md index 274360be1b076..bbdb34bc15da1 100644 --- a/solution/2300-2399/2333.Minimum Sum of Squared Difference/README_EN.md +++ b/solution/2300-2399/2333.Minimum Sum of Squared Difference/README_EN.md @@ -5,8 +5,9 @@ edit_url: https://github.com/doocs/leetcode/edit/main/solution/2300-2399/2333.Mi rating: 2011 source: Biweekly Contest 82 Q3 tags: + - Greedy - Array - - Math + - Binary Search - Sorting - Heap (Priority Queue) --- diff --git a/solution/2300-2399/2336.Smallest Number in Infinite Set/README.md b/solution/2300-2399/2336.Smallest Number in Infinite Set/README.md index 63504a6dfc7ab..09264bdc2f005 100644 --- a/solution/2300-2399/2336.Smallest Number in Infinite Set/README.md +++ b/solution/2300-2399/2336.Smallest Number in Infinite Set/README.md @@ -7,6 +7,7 @@ source: 第 301 场周赛 Q2 tags: - 设计 - 哈希表 + - 有序集合 - 堆（优先队列） --- diff --git a/solution/2300-2399/2336.Smallest Number in Infinite Set/README_EN.md b/solution/2300-2399/2336.Smallest Number in Infinite Set/README_EN.md index dbbe5ddd9f4e3..c047aa8ecf98c 100644 --- a/solution/2300-2399/2336.Smallest Number in Infinite Set/README_EN.md +++ b/solution/2300-2399/2336.Smallest Number in Infinite Set/README_EN.md @@ -7,6 +7,7 @@ source: Weekly Contest 301 Q2 tags: - Design - Hash Table + - Ordered Set - Heap (Priority Queue) --- diff --git a/solution/2400-2499/2416.Sum of Prefix Scores of Strings/README.md b/solution/2400-2499/2416.Sum of Prefix Scores of Strings/README.md index e0a0756216139..1274cc2d19475 100644 --- a/solution/2400-2499/2416.Sum of Prefix Scores of Strings/README.md +++ b/solution/2400-2499/2416.Sum of Prefix Scores of Strings/README.md @@ -337,6 +337,53 @@ function sumPrefixScores(words: string[]): number[] { } ``` +#### JavaScript + +```js +class Trie { + constructor() { + this.children = {}; + this.cnt = 0; + } + + insert(w) { + let node = this; + for (const c of w) { + if (!node.children[c]) { + node.children[c] = new Trie(); + } + node = node.children[c]; + node.cnt++; + } + } + + search(w) { + let node = this; + let ans = 0; + for (const c of w) { + if (!node.children[c]) { + return ans; + } + node = node.children[c]; + ans += node.cnt; + } + return ans; + } +} + +/** + * @param {string[]} words + * @return {number[]} + */ +var sumPrefixScores = function (words) { + const trie = new Trie(); + for (const w of words) { + trie.insert(w); + } + return words.map(w => trie.search(w)); +}; +``` + diff --git a/solution/2400-2499/2416.Sum of Prefix Scores of Strings/README_EN.md b/solution/2400-2499/2416.Sum of Prefix Scores of Strings/README_EN.md index 808ab3f98788c..e5cb5b9c96fc9 100644 --- a/solution/2400-2499/2416.Sum of Prefix Scores of Strings/README_EN.md +++ b/solution/2400-2499/2416.Sum of Prefix Scores of Strings/README_EN.md @@ -337,6 +337,53 @@ function sumPrefixScores(words: string[]): number[] { } ``` +#### JavaScript + +```js +class Trie { + constructor() { + this.children = {}; + this.cnt = 0; + } + + insert(w) { + let node = this; + for (const c of w) { + if (!node.children[c]) { + node.children[c] = new Trie(); + } + node = node.children[c]; + node.cnt++; + } + } + + search(w) { + let node = this; + let ans = 0; + for (const c of w) { + if (!node.children[c]) { + return ans; + } + node = node.children[c]; + ans += node.cnt; + } + return ans; + } +} + +/** + * @param {string[]} words + * @return {number[]} + */ +var sumPrefixScores = function (words) { + const trie = new Trie(); + for (const w of words) { + trie.insert(w); + } + return words.map(w => trie.search(w)); +}; +``` + diff --git a/solution/2400-2499/2416.Sum of Prefix Scores of Strings/Solution.js b/solution/2400-2499/2416.Sum of Prefix Scores of Strings/Solution.js new file mode 100644 index 0000000000000..944fd9f535995 --- /dev/null +++ b/solution/2400-2499/2416.Sum of Prefix Scores of Strings/Solution.js @@ -0,0 +1,42 @@ +class Trie { + constructor() { + this.children = {}; + this.cnt = 0; + } + + insert(w) { + let node = this; + for (const c of w) { + if (!node.children[c]) { + node.children[c] = new Trie(); + } + node = node.children[c]; + node.cnt++; + } + } + + search(w) { + let node = this; + let ans = 0; + for (const c of w) { + if (!node.children[c]) { + return ans; + } + node = node.children[c]; + ans += node.cnt; + } + return ans; + } +} + +/** + * @param {string[]} words + * @return {number[]} + */ +var sumPrefixScores = function (words) { + const trie = new Trie(); + for (const w of words) { + trie.insert(w); + } + return words.map(w => trie.search(w)); +}; diff --git a/solution/3100-3199/3128.Right Triangles/README.md b/solution/3100-3199/3128.Right Triangles/README.md index d105cd34aae93..11ed741a8974d 100644 --- a/solution/3100-3199/3128.Right Triangles/README.md +++ b/solution/3100-3199/3128.Right Triangles/README.md @@ -24,13 +24,9 @@ tags:给你一个二维 boolean 矩阵
-grid。请你返回使用
- -grid中的 3 个元素可以构建的 直角三角形 数目，且满足 3 个元素值 都 为 1 。注意：
+如果
-grid的 3 个元素的集合中，一个元素与另一个元素在 同一行，并且与第三个元素在 同一列，则该集合是一个 直角三角形。3 个元素 不必 彼此相邻。-
+- 如果
-grid中 3 个元素满足：一个元素与另一个元素在 同一行，同时与第三个元素在 同一列 ，那么这 3 个元素称为一个 直角三角形 。这 3 个元素互相之间不需要相邻。请你返回使用
grid中的 3 个元素可以构建的 直角三角形 数目，且满足 3 个元素值 都 为 1 。diff --git a/solution/3100-3199/3128.Right Triangles/README_EN.md b/solution/3100-3199/3128.Right Triangles/README_EN.md index ed41f2c70beaf..cf562f0c62aa5 100644 --- a/solution/3100-3199/3128.Right Triangles/README_EN.md +++ b/solution/3100-3199/3128.Right Triangles/README_EN.md @@ -24,13 +24,9 @@ tags:
You are given a 2D boolean matrix
-grid.Return an integer that is the number of right triangles that can be made with the 3 elements of
+gridsuch that all of them have a value of 1.A collection of 3 elements of
-gridis a right triangle if one of its elements is in the same row with another element and in the same column with the third element. The 3 elements may not be next to each other.Note:
- --
+- A collection of 3 elements of
-gridis a right triangle if one of its elements is in the same row with another element and in the same column with the third element. The 3 elements do not have to be next to each other.Return an integer that is the number of right triangles that can be made with 3 elements of
gridsuch that all of them have a value of 1.
Example 1:
@@ -39,19 +35,19 @@ tags:@@ -59,19 +55,39 @@ tags:
- 0 +0 1 -0 +0 - 0 +0 1 1 - 0 -1 -0 +0 +1 +0 + +
- 0 -1 -0 +0 +1 +0 - 0 +0 1 1 - + +0 +0 1 -0 +0 ++ +
@@ -84,7 +100,7 @@ tags:+ +0 +1 +0 ++ +0 +1 +1 ++ 0 +1 +0 Explanation:
-There are two right triangles.
+There are two right triangles with elements of the value 1. Notice that the blue ones do not form a right triangle because the 3 elements are in the same column.
Example 2:
@@ -93,22 +109,22 @@ tags:@@ -121,7 +137,7 @@ tags:
- 1 -0 -0 -0 +1 +0 +0 +0 - 0 -1 -0 -1 +0 +1 +0 +1 - 1 -0 -0 -0 +1 +0 +0 +0 Explanation:
-There are no right triangles.
+There are no right triangles with elements of the value 1. Notice that the blue ones do not form a right triangle.
Example 3:
@@ -131,18 +147,18 @@ tags:1 -0 +0 1 1 -0 -0 +0 +0 - @@ -151,18 +167,18 @@ tags:1 -0 -0 +1 +0 +0 1 -0 +0 1 - 1 -0 -0 +1 +0 +0 @@ -171,11 +187,11 @@ tags: 1 -0 -0 +0 +0 Input: grid = [[1,0,1],[1,0,0],[1,0,0]]
-Output: 2
+Output: 2
Explanation:
-There are two right triangles.
+There are two right triangles with elements of the value 1.
diff --git a/solution/3200-3299/3271.Hash Divided String/README.md b/solution/3200-3299/3271.Hash Divided String/README.md index a56d69b38c787..4d8c6b7852032 100644 --- a/solution/3200-3299/3271.Hash Divided String/README.md +++ b/solution/3200-3299/3271.Hash Divided String/README.md @@ -27,7 +27,7 @@ tags:
- 一个字符的 哈希值 是它在 字母表 中的下标（也就是
-'a' → 0，'b' → 1，... ，'z' → 25）。- 将子字符串中字幕的 哈希值 求和。
+- 将子字符串中字母的 哈希值 求和。
- 将和对 26 取余，将结果记为
hashedChar。- 找到小写字母表中
hashedChar对应的字符。- 将该字符添加到
diff --git a/solution/3200-3299/3273.Minimum Amount of Damage Dealt to Bob/README.md b/solution/3200-3299/3273.Minimum Amount of Damage Dealt to Bob/README.md index 9ba6bf2d67e5d..662c5ea95ae0b 100644 --- a/solution/3200-3299/3273.Minimum Amount of Damage Dealt to Bob/README.md +++ b/solution/3200-3299/3273.Minimum Amount of Damage Dealt to Bob/README.md @@ -26,7 +26,7 @@ tags:result的末尾。每一秒中，在敌人对 Bob 造成伤害 之后 ，Bob 会选择 一个 还活着的敌人进行攻击，该敌人的健康值减少
-power。请你返回 Bob 将 所有
+n个敌人都消灭之前，最少 会收到多少伤害。请你返回 Bob 将 所有
n个敌人都消灭之前，最少 会受到多少伤害。diff --git a/solution/README.md b/solution/README.md index 78fe9d8fb8acf..679ab18b8899d 100644 --- a/solution/README.md +++ b/solution/README.md @@ -2343,10 +2343,10 @@ | 2330 | [验证回文串 IV](/solution/2300-2399/2330.Valid%20Palindrome%20IV/README.md) | `双指针`,`字符串` | 中等 | 🔒 | | 2331 | [计算布尔二叉树的值](/solution/2300-2399/2331.Evaluate%20Boolean%20Binary%20Tree/README.md) | `树`,`深度优先搜索`,`二叉树` | 简单 | 第 82 场双周赛 | | 2332 | [坐上公交的最晚时间](/solution/2300-2399/2332.The%20Latest%20Time%20to%20Catch%20a%20Bus/README.md) | `数组`,`双指针`,`二分查找`,`排序` | 中等 | 第 82 场双周赛 | -| 2333 | [最小差值平方和](/solution/2300-2399/2333.Minimum%20Sum%20of%20Squared%20Difference/README.md) | `数组`,`数学`,`排序`,`堆（优先队列）` | 中等 | 第 82 场双周赛 | +| 2333 | [最小差值平方和](/solution/2300-2399/2333.Minimum%20Sum%20of%20Squared%20Difference/README.md) | `贪心`,`数组`,`二分查找`,`排序`,`堆（优先队列）` | 中等 | 第 82 场双周赛 | | 2334 | [元素值大于变化阈值的子数组](/solution/2300-2399/2334.Subarray%20With%20Elements%20Greater%20Than%20Varying%20Threshold/README.md) | `栈`,`并查集`,`数组`,`单调栈` | 困难 | 第 82 场双周赛 | | 2335 | [装满杯子需要的最短总时长](/solution/2300-2399/2335.Minimum%20Amount%20of%20Time%20to%20Fill%20Cups/README.md) | `贪心`,`数组`,`排序`,`堆（优先队列）` | 简单 | 第 301 场周赛 | -| 2336 | [无限集中的最小数字](/solution/2300-2399/2336.Smallest%20Number%20in%20Infinite%20Set/README.md) | `设计`,`哈希表`,`堆（优先队列）` | 中等 | 第 301 场周赛 | +| 2336 | [无限集中的最小数字](/solution/2300-2399/2336.Smallest%20Number%20in%20Infinite%20Set/README.md) | `设计`,`哈希表`,`有序集合`,`堆（优先队列）` | 中等 | 第 301 场周赛 | | 2337 | [移动片段得到字符串](/solution/2300-2399/2337.Move%20Pieces%20to%20Obtain%20a%20String/README.md) | `双指针`,`字符串` | 中等 | 第 301 场周赛 | | 2338 | [统计理想数组的数目](/solution/2300-2399/2338.Count%20the%20Number%20of%20Ideal%20Arrays/README.md) | `数学`,`动态规划`,`组合数学`,`数论` | 困难 | 第 301 场周赛 | | 2339 | [联赛的所有比赛](/solution/2300-2399/2339.All%20the%20Matches%20of%20the%20League/README.md) | `数据库` | 简单 | 🔒 | diff --git a/solution/README_EN.md b/solution/README_EN.md index 92a4abf9bf885..188c018c69288 100644 --- a/solution/README_EN.md +++ b/solution/README_EN.md @@ -2341,10 +2341,10 @@ Press Control + F(or Command + F on | 2330 | [Valid Palindrome IV](/solution/2300-2399/2330.Valid%20Palindrome%20IV/README_EN.md) | `Two Pointers`,`String` | Medium | 🔒 | | 2331 | [Evaluate Boolean Binary Tree](/solution/2300-2399/2331.Evaluate%20Boolean%20Binary%20Tree/README_EN.md) | `Tree`,`Depth-First Search`,`Binary Tree` | Easy | Biweekly Contest 82 | | 2332 | [The Latest Time to Catch a Bus](/solution/2300-2399/2332.The%20Latest%20Time%20to%20Catch%20a%20Bus/README_EN.md) | `Array`,`Two Pointers`,`Binary Search`,`Sorting` | Medium | Biweekly Contest 82 | -| 2333 | [Minimum Sum of Squared Difference](/solution/2300-2399/2333.Minimum%20Sum%20of%20Squared%20Difference/README_EN.md) | `Array`,`Math`,`Sorting`,`Heap (Priority Queue)` | Medium | Biweekly Contest 82 | +| 2333 | [Minimum Sum of Squared Difference](/solution/2300-2399/2333.Minimum%20Sum%20of%20Squared%20Difference/README_EN.md) | `Greedy`,`Array`,`Binary Search`,`Sorting`,`Heap (Priority Queue)` | Medium | Biweekly Contest 82 | | 2334 | [Subarray With Elements Greater Than Varying Threshold](/solution/2300-2399/2334.Subarray%20With%20Elements%20Greater%20Than%20Varying%20Threshold/README_EN.md) | `Stack`,`Union Find`,`Array`,`Monotonic Stack` | Hard | Biweekly Contest 82 | | 2335 | [Minimum Amount of Time to Fill Cups](/solution/2300-2399/2335.Minimum%20Amount%20of%20Time%20to%20Fill%20Cups/README_EN.md) | `Greedy`,`Array`,`Sorting`,`Heap (Priority Queue)` | Easy | Weekly Contest 301 | -| 2336 | [Smallest Number in Infinite Set](/solution/2300-2399/2336.Smallest%20Number%20in%20Infinite%20Set/README_EN.md) | `Design`,`Hash Table`,`Heap (Priority Queue)` | Medium | Weekly Contest 301 | +| 2336 | [Smallest Number in Infinite Set](/solution/2300-2399/2336.Smallest%20Number%20in%20Infinite%20Set/README_EN.md) | `Design`,`Hash Table`,`Ordered Set`,`Heap (Priority Queue)` | Medium | Weekly Contest 301 | | 2337 | [Move Pieces to Obtain a String](/solution/2300-2399/2337.Move%20Pieces%20to%20Obtain%20a%20String/README_EN.md) | `Two Pointers`,`String` | Medium | Weekly Contest 301 | | 2338 | [Count the Number of Ideal Arrays](/solution/2300-2399/2338.Count%20the%20Number%20of%20Ideal%20Arrays/README_EN.md) | `Math`,`Dynamic Programming`,`Combinatorics`,`Number Theory` | Hard | Weekly Contest 301 | | 2339 | [All the Matches of the League](/solution/2300-2399/2339.All%20the%20Matches%20of%20the%20League/README_EN.md) | `Database` | Easy | 🔒 |